Kaggleのtitanic問題で上位10%に入るまでの環境構築とデータ分析

Article

2016.10.22

本記事のコード/ご参照
・本記事の全体のコードのnotebookを以下にアップしております。あわせてご参照くださいませ。
“Kaggle titanic_tutorial_code”

・本記事含むKaggleやデータ分析初学者向けのチュートリアル解説本を執筆しました。あわせてご参照くださいませ。

※本記事のコードや環境構築の詳細手順を記載した書籍となります。
『Pythonで動かして学ぶ！Kaggleデータ分析入門』

※はじめに
本記事は2020年の上記書籍発売に合わせて内容を加筆・修正しました。そのため執筆当初と内容が異なる箇所がございます。またKaggleあるいはデータ分析における最初のチュートリアルとしてtitanicは長らく親しまれておりましたが、下記3点の現状があることをご認識いただいた上で取り組まれるのが良いかと思います。

・データ数が少なくOverfit（過学習）しやすい
・あまりに有名な問題であり全正解データが公開されている。そのためLeaderBoard（順位）が機能していない。
・現在Kaggleではplaygroundとしてよりデータ数が多く豊富な種類の様々なテーブルデータのチュートリアルコンペを開催している。

とはいえ、Python初学者がまずはとにかく手元でデータ分析する手順をコードを動かしながら短時間で体験してみたいということでしたら、その候補の一つとしては良いかもしれません。

近年各社においてデータサイエンス系人材の採用が活発であり、学生時代あるいは企業の新人ながらデータサイエンティストとして活躍することは珍しくありません。
一方でプログラミングなどに触れてこなかった方々もPythonを用いたデータ分析などに興味をもつ機会も多いと思います。
本記事はデータ分析初学者の方に向けてKaggleというデータ解析コンペプラットフォームを通じてデータ分析のチュートリアルをご紹介することを目的としています。
※ただしPythonの基礎的な知識は持ち合わせている前提とします。

この記事を読むことでデータ初学者の方々でも
「3,000、4,000、、、5,000人か（分析サンプルが）。5分、いや、3分で(分析を)片付けてやろう。(タイピングは)右手のみで十分だ」
といった発言ができるようになることを期待します。
※もちろん冗談です。この記事の内容でそのような発言を行えば中二病と思われるだけならまだしもとても痛い目を見ることになるでしょう。

目次
1) Kaggleとは
2) titanicチュートリアル
3) 分析環境
4) データ探索
5) データ分析・前処理
6) モデリング
7) 結果
8) 所感

| (1) Kaggleとは

Kaggleは、2010年4月に米国においてAnthony Goldbloom、Ben Hamner 両氏によりスタートしたデータ分析コンペのプラットフォームです。2017年にGoogleに買収され、Google擁するAlphabet傘下となりました。これまでに世界中のデータサイエンティスト10万人以上が参加しており、コンスタントに10前後のコンペが開催されております。

Kaggleの各コンペでは、解くべき課題と評価指標、実際のデータが与えられます。参加者は与えられたデータをもとに期日内に様々な分析を行い、精度の高い予測などを行うことを目指します。自分が分析した結果はKaggleに投稿するとオンラインで数分ほどで採点され（コンペにより採点にかかる時間は異なります）、評価指標に基づいて参加者間で順位付けされます（この順位表はLeaderBoardと呼ばれます）。

一方で、Kaggleではお互いを高め合うコミュニティ的な側面もあります。お互いのコンペでの気づきを投稿し合う「Discussion」機能、自分の一連の手順を実際のプログラムとして共有する「Notebook」機能があり、さらにそれらにコメントおよび「Vote（投票）」ができます。自分のデータサイエンス力の現状を確かめるだけではなく、他の人の最新ナレッジ・スキルを学べることも魅力の1つです。

Kaggleの各コンペでは、Private Leaderboardの最終順位結果に基づいてGold、Silver、Bronzeといったメダルや賞金が授与されます（メダルや賞金授与は、対象コンペのみとなります）。各コンペ参加人数によって、メダル授与条件は異なるのですが、Kaggle公式ページの記載の通り、例えば参加者が1,000人のコンペの場合、Top10%が「Bronze」、Top5%が「Silver」、Top10位以内が「Gold」となります。

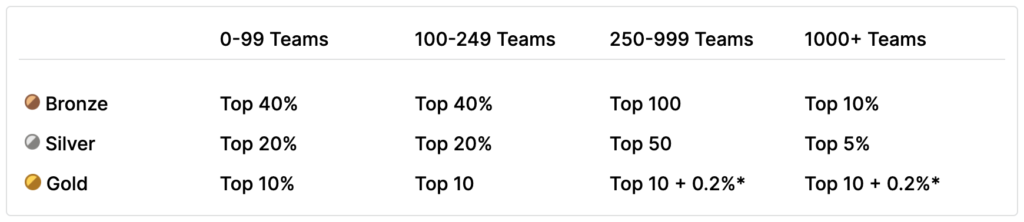
さらに、各コンペのメダル実績に基づいて、称号および総合ランキングが付与されます。たとえば「Competitions」（コンペのランキングによるもの）の称号では、Bronze以上のメダル2つでKaggle Expert になり、Goldメダル1つとSilverメダル2つ以上の実績でKaggle Master になります。さらに、Goldメダル５つ以上（かつ1人（ソロ）でのGoldメダル1つ以上）でGrandmasterになります。

| (2) titanicチュートリアル

Kaggleでは企業からの問題以外に、賞金なしのKaggleからのチュートリアルチャレンジもあります。titanicチュートリアルは、その一つです。1912年に起きた、かの有名なタイタニック号沈没事件を題材に、乗客の年齢、性別、社会階級ランク、などのデータから、生死を予測する、というものです。

ちなみに、タイタニック号沈没事件は、”若い乗客、女性の乗客から先に救命ボートに乗せた”、などの史実があり、上記乗客のプロファイルデータからある程度生死を予測できることから、よくデータ分析の題材に用いられますので、ご存知の方も多いかと思います。
※Rのデフォルトデータセットにも含まれております。

データセットは下記の通りです。

PassengerID	乗客ID
survival	生死(0 = No; 1 = Yes)※trainデータのみに存在。testデータのこの値を予測する。
pclass	乗客の社会階級(1 = 1st(High); 2 = 2nd(Middle); 3 = 3rd(Low))
name	Name
sex	性別
age	年齢
sibsp	乗船している夫婦、兄弟姉妹の数
parch	乗船している親、子供の数
ticket	チケットNo
fare	乗船料金
cabin	船室
embarked	乗船場所(C = Cherbourg; Q = Queenstown; S = Southampton)

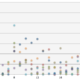
ちなみにKaggleのtitanicチュートリアルチャレンジは2016/10/21時点で、5,590人が参加しております。平均精度は、0.769、予測精度0.6〜0.8の間に参加者のおおよそ80%を占める状況となります。（時期によって異なります）

※Kaggle titanicチュートリアルチャレンジにおける予測精度ごとの人数分布(横軸：予測精度、縦軸：人数)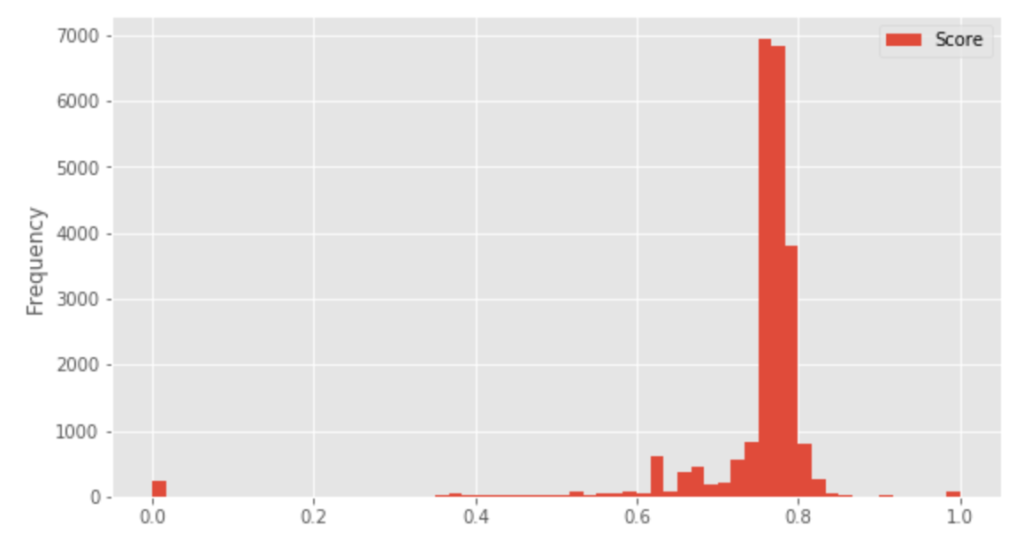

| (3) 分析環境

Pythonの実行は、ターミナル上でプログラムファイルを指定して行うこともできますが、データ分析において、試行錯誤しながら処理を進める場合、Jupyter Notebookを使用すると便利です。

Jupyter Notebookは、Webブラウザ上で動作する対話的プログラム実行環境となります。複数のプログラム言語をカバーしている点、オープンソースのため無料で使用することができる点、プログラムと併せて図やテキストなどの注釈を入れて、それらを.ipynb形式で書き出して他の人に共有できる点などから、多くのデータ分析の現場で使用されております。

ローカルPCで分析環境を構築する場合、気を付けたいことは、いつでも環境構築をやり直せるようにしておくことです。Python自体もそうですし、分析のためのPythonパッケージは都度更新され、各パッケージが依存関係にあることも多々あります。そのため、度々パッケージのインストール・更新を行うことになりますが、これまで問題なく動作していたコードやパッケージがバージョンによってうまく動かないということがしばしば起こり得ます。

そのため手元のPCにそのままPythonを入れず、仮想環境などを構築して、各バージョンを切り替え、もしうまく動作しなくなったら、いつでももとに戻せる方法を推奨します。仮想環境の構築にはAnacondaやvirtualenv、サーバを仮想化する（コンテナ化する）Dockerを用いた方法など様々ありますが、ここでは仮想環境ではないものの、バージョン管理ツールとして定評のあるpyenvを用いた方法について解説します。以降はmacでの環境構築について述べますが、windowsではpyenv-winのインストール手順を参照してください。またもしこの手順にハードルを感じる場合はAnacondaを用いた方法やKaggle自体の分析環境を使用することもできます。

まずターミナルを起動し、下記のように入力して実行しpyenvをインストールします。

brew install pyenv

1	brew install pyenv

次に、pyenvにパスを通すために、次のコマンドを入力して実行します。（vimの操作に慣れていない方も、とりあえず、次の手順に従って読み進めてください）。

vim ~/.bash_profile

1	vim ~/.bash_profile

vimが立ち上がり、.bash_profileの編集画面になりますので、［i］キーを押して編集モードにした後、次の内容を入力してください。

export PYENV_ROOT="$HOME/.pyenv"
export PATH="$PYENV_ROOT/bin:$PATH"
eval "$(pyenv init -)"

export PYENV_ROOT="$HOME/.pyenv"

export PATH="$PYENV_ROOT/bin:$PATH"

eval "$(pyenv init -)"

入力し終わったら、［esc］キーを押して、編集モードを終えた後、「:wq」（vimコマンドで、「wq」は保存して終了の意味）と入力しましょう。vimの画面から通常のターミナル画面に戻ったら、次のコマンドを入力して実行し、先ほどの変更を適用します。これで、準備は整いました。

source ~/.bash_profile

1	source ~/.bash_profile

pyenvでインストールできるPythonのバージョンを次のコマンドを入力して実行し、確認してみましょう。

pyenv install --list

1	pyenv install --list

次に、表示されたリストの中から、任意のバージョンのPythonをインストールします。たとえば「3.7.6」を指定する場合、次のコマンドを入力して実行します。終了するまで少し時間がかかります。

pyenv install 3.7.6

1	pyenv install 3.7.6

pyenv経由で入っているバージョンを一覧で表示するには、次のコマンドを入力して実行します。

pyenv versions

1	pyenv versions

Pythonのバージョンを切り替えたくなった場合は、次のコマンドを入力して実行します。すべてのディレクトリで切り替えたい場合はglobal、現在のディレクトリのみ切り替えたい場合は、localを指定します。

pyenv global 3.7.6

1	pyenv global 3.7.6

Pythonのバージョンを切り替えたら、念のため、次のコマンドを入力して実行し、現在の環境が正しく切り替わっているかを確認します。

python -V

python -V

最後に、Jupyter Notebookをインストールしておきましょう。

pip install --upgrade pip
pip install jupyter

1 2	pip install --upgrade pip pip install jupyter

Jupyter Notebookを起動するには次のコマンドを入力して実行します。ブラウザが立ち上がってセルにコードを記述できるようになります。

jupyter notebook

1	jupyter notebook

※記事冒頭の書籍にてより詳細な環境構築の方法について記載しております。

| (4) データ探索

※以下、処理やコードを抜粋しながら紹介いたします。全体のコードは記事冒頭にてご紹介しているnotebookか書籍をご参考くださいませ。

では、titanicチュートリアルチャレンジを始めてみます。
まずは、Kaggleにサインインして”Titanic:MachineLearning from Disaster”のコンペのページにアクセスし、右上の「Join Competition」をクリックしましょう。「Please read and accept the competition rules」の画面が表示されたら「I Understand and Accept」をクリックします。コンペに参加したら、「Data」タブをクリックしましょう。以下の3つのデータがあります。ローカル環境で分析を行う場合、「Download All」をクリックすることでまとめてtitanic.zipという名前でダウンロードされますので、解凍しておきます。

・train.csv：学習データ
・test.csv：テストデータ
・gender_submission.csv：sample submissionデータ

まずはjupyter notebookでデータを読み込んで、形式を確認してみます。そのためにターミナルを起動してPythonのライブラリ（必要な機能がまとまったもの）をインストールします。pandasはDataFrameと呼ばれる数表などのデータ構造を扱うためのライブラリ、NumPyは数理計算を行うためのライブラリとなります。

pip install pandas
pip install numpy

1 2	pip install pandas pip install numpy

上記完了しましたら、下記でライブラリをプログラムに読み込みます。

import pandas as pd
import numpy as np

1 2	import pandas as pd import numpy as np

これでデータを読み込む準備ができましたので、下記のようにしてtrain.csvデータを読み込んでみます。（notebookと同じフォルダにデータが有る場合。通常は「notebook」「data」などフォルダを分けて管理します。）

train_df = pd.read_csv("train.csv")
test_df = pd.read_csv("test.csv")
train_df

train_df = pd.read_csv("train.csv")

test_df = pd.read_csv("test.csv")

train_df

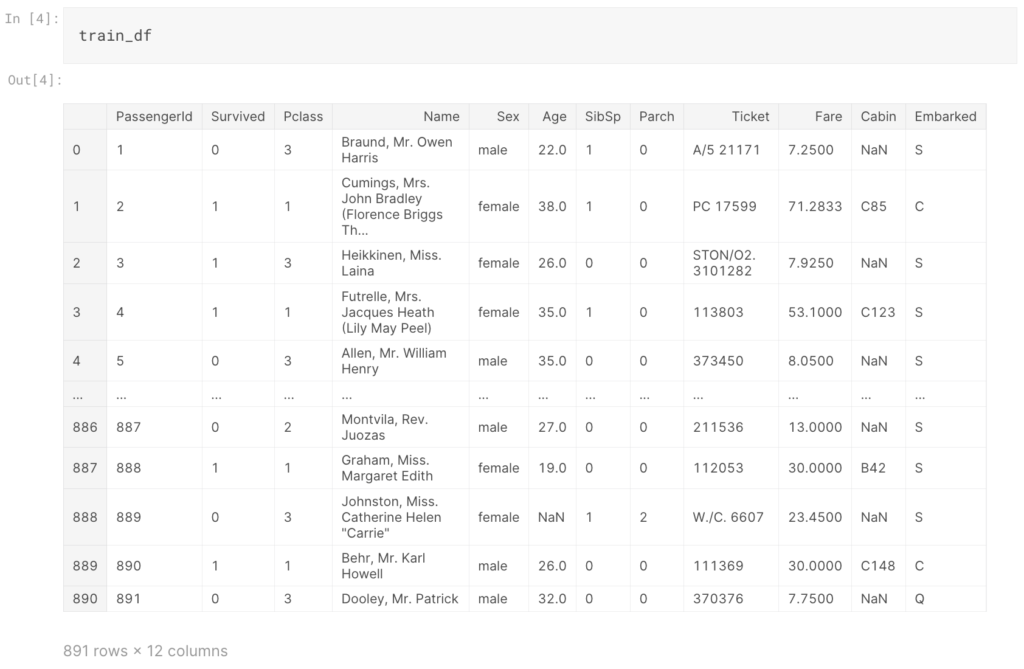
次に、行数・列数を確認します。

print(train_df.shape)
print(test_df.shape)

1 2	print(train_df.shape) print(test_df.shape)

上記実行すると、(891,12)、(418,11)と表示されるかと思います。学習データは891行で12列のデータ、テストデータは418行で目的変数（Survived）を除く11行のデータとわかります。

またデータの型も確認してみます。型とは、そのデータが数値なのか文字列なのかなどを表すものであり、数値には、整数であるint型や、小数であるfloat型があります。intやfloatの後の数字はbit数を表し、数が大きいほど表現できる数の範囲が大きくなります。

train_df.dtypes

1	train_df.dtypes

参照結果を見てみるとName、Sex、Ticket、Cabin、Embarkedはobject型（文字列など）、それ以外はintやfloatの数値データのようです。ただし、数値データについては注意が必要です。一般的に数値データには、質的変数、量的変数という2種類のものがあります。質的変数とは、「分類のための数値であり、間隔には意味がないもの」となります。Pclass（チケットクラス）、などの数値データは、質的変数となります。一方、量的変数は、Age（年齢）、Fare（チケット料金）のようなものであり「間隔に意味がある数値」となります。量的変数はさらに間隔尺度と比例尺度に分類できます。

それからデータ内の数値データの概要を確認しておきましょう。

train_df.describe()

1	train_df.describe()

上記により、データ内の各変数におけるcount（データの個数）、mean（平均）、std（標準偏差）、min（最小値）、25%（1/4分位数）、50%（中央値）、75%（3/4分位数）、max（最大値）などがわかります。これらをtrainデータとtestデータで実行し、分布がおおよそ同じかを確認しておきます。

さらに各変数において欠損がどれくらいあるかを確認しておきます。

train_df.isnull().sum()

1	train_df.isnull().sum()

AgeおよびCabinについて欠損値が多く含まれていることが確認できます。

ここから次の処理に進む前に、カテゴリ変数をダミー変数化しておきます。相関係数や機械学習などの処理は数値データに変換することで取り扱いやすくなります（テキストのままで実行可能な処理もあります）。ここではSex(性別)、Embarked(乗船場所)を、ダミー変数化しておきます。

train_df = pd.get_dummies(train_df, columns=["Sex"],drop_first=True)
train_df = pd.get_dummies(train_df_corr, columns=["Embarked"])

1 2	train_df = pd.get_dummies(train_df, columns=["Sex"],drop_first=True) train_df = pd.get_dummies(train_df_corr, columns=["Embarked"])

ここで、予測したい対象である目的変数のSurvivedと各変数の相関行列を可視化してみます。そのためにまずは可視化のためのライブラリをインストールします。

pip install matplotlib
pip install seaborn

1 2	pip install matplotlib pip install seaborn

インストールが完了したら、下記のようにしてライブラリをインポート、表示設定を指定します。

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("ggplot")

%matplotlib inline

import matplotlib.pyplot as plt

import seaborn as sns

plt.style.use("ggplot")

では相関行列を作成し、表示してみます。

train_corr = train_df.corr()

plt.figure(figsize=(9, 9))
sns.heatmap(train_corr, vmax=1, vmin=-1, center=0, annot=True)

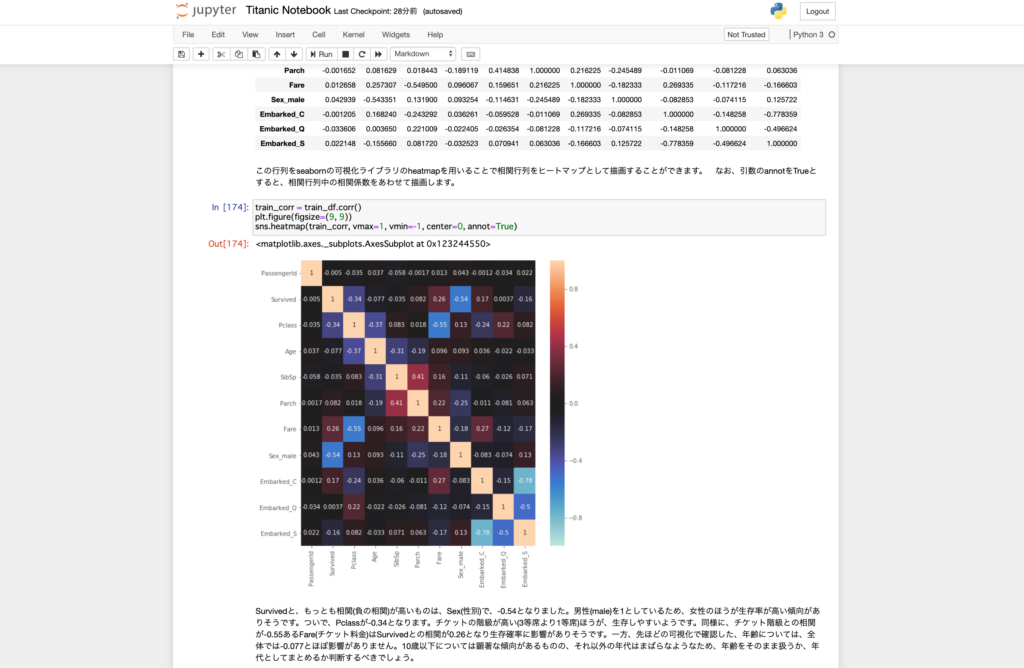
train_corr = train_df.corr()

plt.figure(figsize=(9, 9))

sns.heatmap(train_corr, vmax=1, vmin=-1, center=0, annot=True)

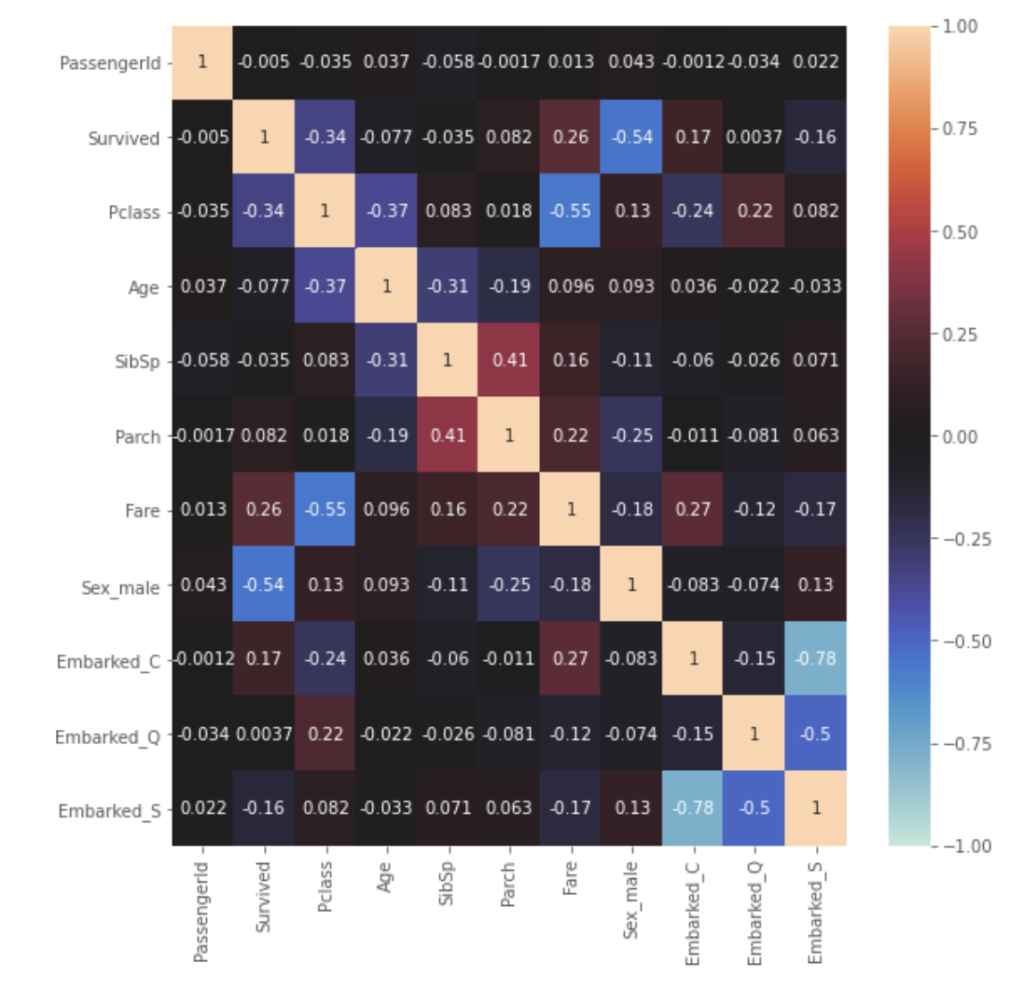
Survivedと、もっとも相関（負の相関）が高いものは、Sex_maleで-0.54となりました。男性（male）を1としているため、相関係数がマイナスであることからも、男性のほうが生存率が低く、女性のほうが生存率が高い傾向がありそうです。ついで、Pclassが-0.34となります。チケットの階級が高い（3等席より1等席）ほうが、生存しやすいようです。またFareはSurvivedとの相関が0.26となり生存確率に影響がありそうです。一方、Ageについては、全体では-0.077とSurvivedと相関がないようです。しかし本記事では詳細な分析は省略しますが実は年齢は生存予測において非常に重要な変数となります。相関係数はあくまで数値間の上下傾向が一致しているかの指標であることに注意しましょう。そのため年齢をそのまま扱うか、年代としてまとめるか判断するべきでしょう。（実際、10歳以下については他の年代と比較して生存率が高い傾向があります）

| (5) 前処理

本記事では、特に名前の変数からの特徴量追加について解説します。その他の処理や変数追加については冒頭に記載した全体のnotebookあるいは書籍にて詳細解説しておりますのでご参照くださいませ。

さて、名前は、「苗字」「敬称」「名前」の順に記載されております。ここで、特に「敬称」に注目します。敬称は「Master.」「Mr.」「Miss.」「Mrs.」などがありますが、それぞれ一般的に年齢や性別に関係があります。

実際にそれぞれの敬称の平均値を求めてみましょう。

敬称	備考	平均年齢
master	主に男性の子供に使用される	4.1歳
mr	男性一般に利用される	24.9歳
miss	未婚女性（mrsよりも若い可能性）	17.5歳
mrs	既婚女性(missよりも年齢が高い可能性)	31.1歳

上記のように敬称によって明確に平均年齢に違いがでるようですので（年齢の推計に敬称が利用できる）”mr”、”master”、”miss”、”mrs”のフラグをデータに加えることにします。

名前データからの敬称によるフラグ付けのコードは下記となります。

name_df = train_df["Name"].str.split("[,.]",2,expand=True)
name_df.columns = ["family_name","honorific","name"]

for c in name_df.columns:
  name_df[c] =name_df[c].str.strip()

train_df = pd.concat([train_df, name_df],axis=1)

name_df = train_df["Name"].str.split("[,.]",2,expand=True)

name_df.columns = ["family_name","honorific","name"]

for c in name_df.columns:

name_df[c] =name_df[c].str.strip()

train_df = pd.concat([train_df, name_df],axis=1)

また、名前の苗字から、あるIDと別のIDが”家族”だと推測できますが、家族の同船（1人か家族と一緒か）は本人の生存に関係がある可能性があります。旅行時において家族は、近くで行動していたと思われますし、特に非常事態では一緒に行動し、救命ボートもできるだけ家族一緒に乗りたいのではないでしょうか。そこで家族の同船を変数として追加しておきます。

train_df.loc[train_df["family_num"] ==0, "alone"] = 1
train_df["alone"].fillna(0, inplace=True)

1 2	train_df.loc[train_df["family_num"] ==0, "alone"] = 1 train_df["alone"].fillna(0, inplace=True)

その他、不要な変数の削除や欠損値の処理など全体のコードは冒頭のnotebookあるいは書籍にてご確認くださいませ。

| (6) データ解析・モデリング

KaggleのチュートリアルではよくLightGBMという手法が紹介されることが多いのですが、この記事ではSVM(サポートベクターマシーン)を用いてモデリングすることにします。(今回のケースの場合、精度がよかったので)
※lightGBMを用いたコードは冒頭のnotebookにて紹介しております。

SVMについて簡単にご説明しますと、
・サポートベクトル
・カーネルトリック
という2つの特徴を使用した手法となります。

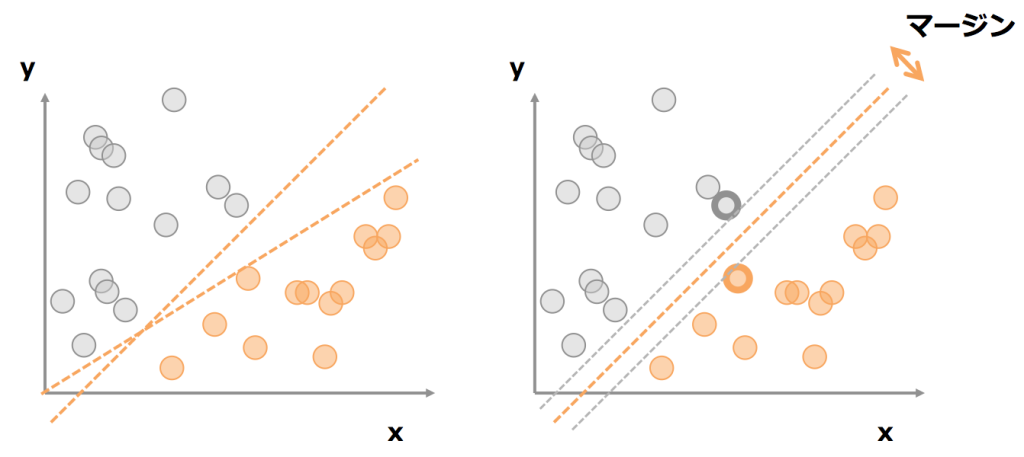
サポートベクトルとは、決定境界(今回では生存した人たちの境界、死亡した人たちの境界)にもっとも近いサンプルのこととなります。
SVMは、このサポートベクトル間のマージンを最大にするように、分離平面を選択する、手法です。
※ちなみに、この分離平面による誤分類のペナルティは変数としてチューニングすることが可能です。
(トレーニングデータセットでの精度の向上を目指すか、汎化性能を高めるか、のトレードオフ)

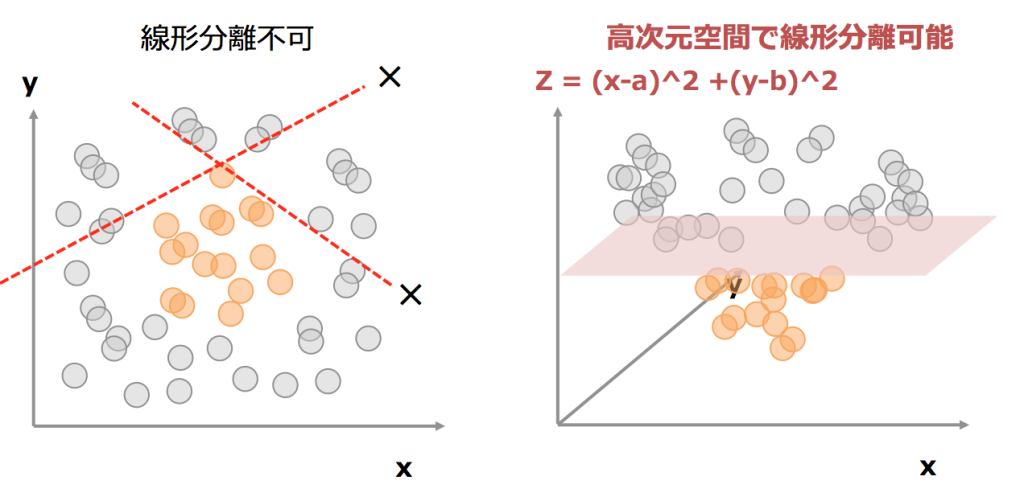
カーネルトリックとは、線形分離ができないデータに関しても高次元に射影することで、高次元空間で分離する手法です。

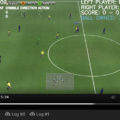
たとえば、左図の場合、線形分離が不可となりますが、中心点をx=a、y=bとすると、Z=(x-a)^2 + (y-b)^2なる新たな次元を設けると、
中心近くはzの値が小さくなり、中心から離れるほどzの値が大きくなりますので、あるzの閾値によって分離することが可能となります。（右図）

Pythonでのコードは下記となります。
※事前に別手法(ランダムフォレスト)で0.7986の予測精度(手元のデータで)が出たので、それ以上だったときの予測精度のパラメータを探索しています。
※クロスバリデーションで、トレーニングデータセットを10分割したときの平均予測精度を出しています。
※SVMに、かける前にpipeline経由の処理でデータを正規化しています。
※X_train2_sur、y_train2_surが、前述の前処理後のデータ

from sklearn.svm import SVC

best_score = 0.7986
for i in range(5,20):
    i = i / 100    
    for j in range(100,250):
        j = j / 100
        clf_svm = SVC(kernel='rbf',random_state=0,gamma=i,C=j)
        pipe_svm = Pipeline([['sc', StandardScaler()],['clf', clf_svm]])
        scores = cross_val_score(estimator=clf_svm,
                                 X=X_train2_sur,
                                 y=y_train2_sur,
                                 cv=10,
                                 scoring='roc_auc')
        if scores.mean() == best_score:
            print("gamma:",i,"C:",j,scores.mean(),"+-",scores.std())

from sklearn.svm import SVC

best_score = 0.7986

for i in range(5,20):

i = i / 100

for j in range(100,250):

j = j / 100

clf_svm = SVC(kernel='rbf',random_state=0,gamma=i,C=j)

pipe_svm = Pipeline([['sc', StandardScaler()],['clf', clf_svm]])

scores = cross_val_score(estimator=clf_svm,

X=X_train2_sur,

y=y_train2_sur,

cv=10,

scoring='roc_auc')

if scores.mean() == best_score:

print("gamma:",i,"C:",j,scores.mean(),"+-",scores.std())

| (7) 結果

予測精度：0.80861
順位：490位 / 5,590人
※2016/10/21時点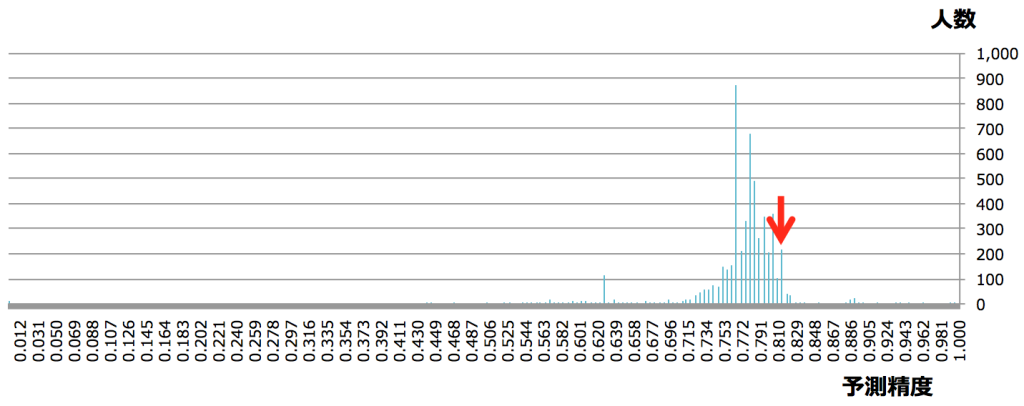

となり、執筆時点で無事上位10%以内(上位9%以内)にランクインできました。ちなみに投稿は何度でも繰り返し行うことができ、通常はコンペ期間内ギリギリまで精度の向上、ランキングの上昇を狙います。
※今回のtitanicはチュートリアルのため、期限は考慮せず。

| (8) 所感

さて、今回Kaggleのチュートリアルのご紹介をしましたが、データ分析において重要な点を下記に整理してみます。

・データを解釈して、意味のあるフラグに分解する。
名前そのものでは、意味のないデータ（しかも非構造化データ）ですが、
“家族”、”敬称からのおおよその年齢”、”敬称からの身分”など、フラグ付けをすることで
意味のある”情報”となります。
データ分析プロセスでは、この手の”データの解釈”が非常に重要と感じます。

・予測精度を1%上げる意味
データ解析コンペでは、予測精度を1%どころか0.1%を争ったりするわけですが、
大手ECサイトですと、レコメンドの精度が1%異なることで、売上に多大な影響が出てしまいます。
一方、実環境では、導入コスト、計算コスト、さらにはデータ入手コストがあるわけでして、
トレードオフは常に気にする必要があります。

・精度をあげる過程で、事象に対する理解を深める。
1%精度を上げるためにデータを深堀する過程で、データの背景にある、
人間の行動、事象の理解が深まることがあります。
そうすると、与えられた問題以外の根源的な示唆が得られることがあります。
※今回の例では、タイタニック号の乗客の生死を予測する問題でしたが、
　そもそも、救助活動はどのような手順にすることが有効か、などの問いへの示唆。

以上となります。
奢れるものは、沈みゆくタイタニック号と同じ運命をたどることになり、そこからの救命ボートはjupyter notebookといえますので、本日もnotebookにしがみつきましょう。

本記事に関する全体コードのnotebookなどは下記にアップしております。あわせてご参照くださいませ。

※本記事のコードや環境構築の詳細手順を記載した書籍となります。
『Pythonで動かして学ぶ！Kaggleデータ分析入門』

関連記事: