Article
本記事のコード/ご参照
・本記事の全体のコードのnotebookを以下にアップしております。あわせてご参照くださいませ。
“Kaggle houseprices-tutorial-code”
・本記事含むKaggleやデータ分析初学者向けのチュートリアル解説本を執筆しました。あわせてご参照くださいませ。 ※本記事のコードや環境構築の詳細手順を記載した書籍となります。
『Pythonで動かして学ぶ！Kaggleデータ分析入門』
・本記事の全体のコードのnotebookを以下にアップしております。あわせてご参照くださいませ。
“Kaggle houseprices-tutorial-code”
・本記事含むKaggleやデータ分析初学者向けのチュートリアル解説本を執筆しました。あわせてご参照くださいませ。 ※本記事のコードや環境構築の詳細手順を記載した書籍となります。
『Pythonで動かして学ぶ！Kaggleデータ分析入門』
※はじめに
本記事は2020年の上記書籍発売に合わせて内容を加筆・修正しました。そのため執筆当初と内容が異なる箇所がございます。
データサイエンティストの業務は華やかなPythonでの機械学習よりもBigQueryなどでの地道なデータ収集・データ集計に時間が割かれるのではと思います。もちろん、機械学習とデータ集計、どちらが華やかなのかには異論があり、芸術的なQueryを目のあたりにして嗚咽を漏らすことはままあるとして。日々の業務がデータ集計の割合が多くとも、最終的な成果は機械学習の出来に左右されることが多く、コンスタントに各手法の扱いに慣れておくことが必要です。
そこで本記事では、データ分析初学者の方やこれからKaggleを始めようと思う方向けにHouse Pricesチュートリアルコンペを通した複数手法のアンサンブルおよびパラメータチューニングについて記載いたします。
| (1) House Pricesチュートリアル House Pricesチュートリアルとは、米国アイオワ州のエイムズという都市の物件価格を予測する問題となります。データは、”築年数”、”設備”、”広さ”、”エリア”、”ガレージに入る車の数”など79個の変数および物件価格による1460戸の学習データが与えられます。そのデータをもとにモデルを作成し、1459戸の家の価格を予測します。評価は平均二乗誤差（RMSE）となり、正解データと予測の誤差が小さいほど上位となります。
注意が必要な点として、本コンペの評価指標は「正解値の対数をとったものと、予測値の対数をとったものの間でのRMSE」であるという点です。背景として、Evaluationの項目に「Taking logs means that errors in predictingexpensive houses and cheap houses will affect the result equally.」（対数をとるのは、価格が高い家の予測誤差も、価格が低い家の予測誤差も等しく結果に影響するようにするため）と記載されています。手元のデータで、予測精度を確認する際には、対数をとることを忘れないようにしましょう。
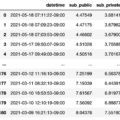
なお、House Prices コンペにおけるLeaderboardの精度の分布は下記のようになります。
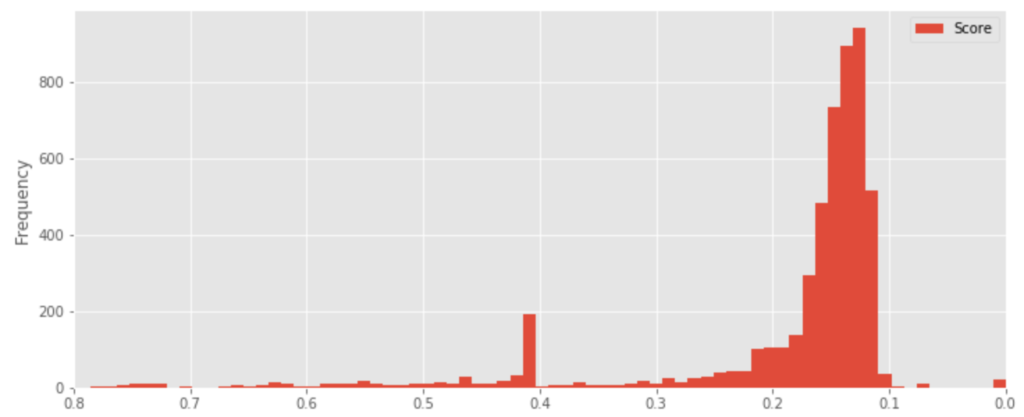
| (2) ベースラインの作成 ※本記事のコードは一部の処理を端折りながら解説しています。全体のコードは冒頭のnotebookをご参照くださいませ。
まずは、データの読み込みから予測まで行うベースラインを作成することにします。ライブラリをインポートしランダムシード（乱数を発生する際の設定。これを設定しないと同じ処理をしても予測結果が異なるようになり処理の検証が困難になる。値は任意の数字で可）を設定しておきます。
|
1 2 3 4 5 6 |
import pandas as pd import pandas as np import randdom np.random.seed(1234) random.seed(1234) |
次に各種データを読み込みます。（下記はnotebookと同じフォルダにデータが有る場合。通常はdataフォルダ、notebookフォルダなど分ける場合が多い）
|
1 2 3 |
train_df = pd.read_csv("./train.csv") test_df = pd.read_csv("./test.csv") submission = pd.read_csv("./sample_submission.csv") |
次に、学習データとテストデータを連結します。これはこのあとの前処理を一括で行うためです。
|
1 |
all_df = pd.concat([train_df, test_df], sort=False).reset_index(drop=True) |
all_dfのobject型のカテゴリ変数を数値に変換していきます。まずはLabelEncoderのライブラリをインポートします。次に、all_dfの中のobject型の変数を取得後、カテゴリ変数を1つずつ呼び出して、欠損値を”missing”に変換後、数値に変換していきます。
|
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.preprocessing import LabelEncoder categories = all_df.columns[all_df.dtypes == "object"] for cat in categories: le = LabelEncoder() print(cat) all_df[cat].fillna("missing", inplace=True) le = le.fit(all_df[cat]) all_df[cat] = le.transform(all_df[cat]) all_df[cat] = all_df[cat].astype("category") |
これでひとまずの処理はできましたので再び、train_dfとtest_dfに戻します。
|
1 2 |
train_df_le = all_df[~all_df["SalePrice"].isnull()] test_df_le = all_df[all_df["SalePrice"].isnull()] |
ここからLightGBMで予測します。LightGBMとは近年Kaggleコンペで非常によく使用されている決定木系の機械学習手法となります。まずは決定木系について説明したあとLightGBMについて簡単に説明します。
決定木とは閾値条件によるデータの分岐を繰り返すことで、回帰や分類をする手法となります。以下の図の例では、「年齢が30歳以上か」「男性か」などの条件を繰り返していき、最終的に各条件の組み合わせによる、生存・死亡の数を表しています。なお、閾値条件は、「ある条件によって、もとのデータが別の性質を持つ2つのデータにうまく分かれたか」を表す指標などによって自動的に決定されていきます。データ分析者は、どの程度まで分岐させるか（木の深さ）、データを分けた時の各グループの最低データ数（葉の数）などを調整していき、分類や予測の精度を向上させていきます。
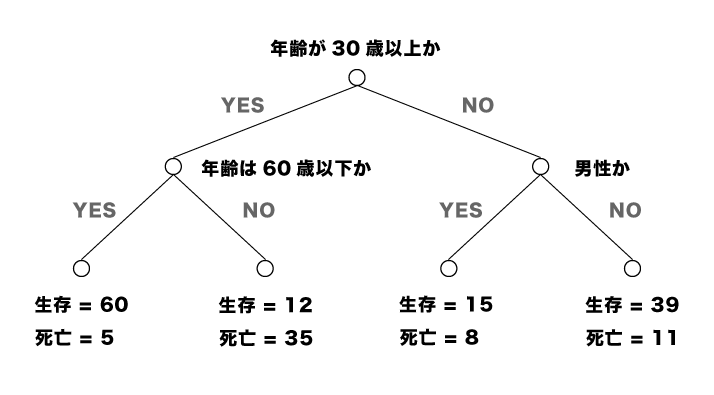
決定木は、アウトプットが条件を組み合わせた木として現れるため、わかりやすく、得られたモデルを簡易に施策などに応用できることから有用ではあるのですが、異常値に弱く、最初の分岐が偏ると以降の分岐がすべて精度の悪いものになってしまいます。そこで近年では決定木を逐次的に更新していくGradient Boosting Decision Treeという手法が提案され、その実装方法の1つがLightGBMとなります。
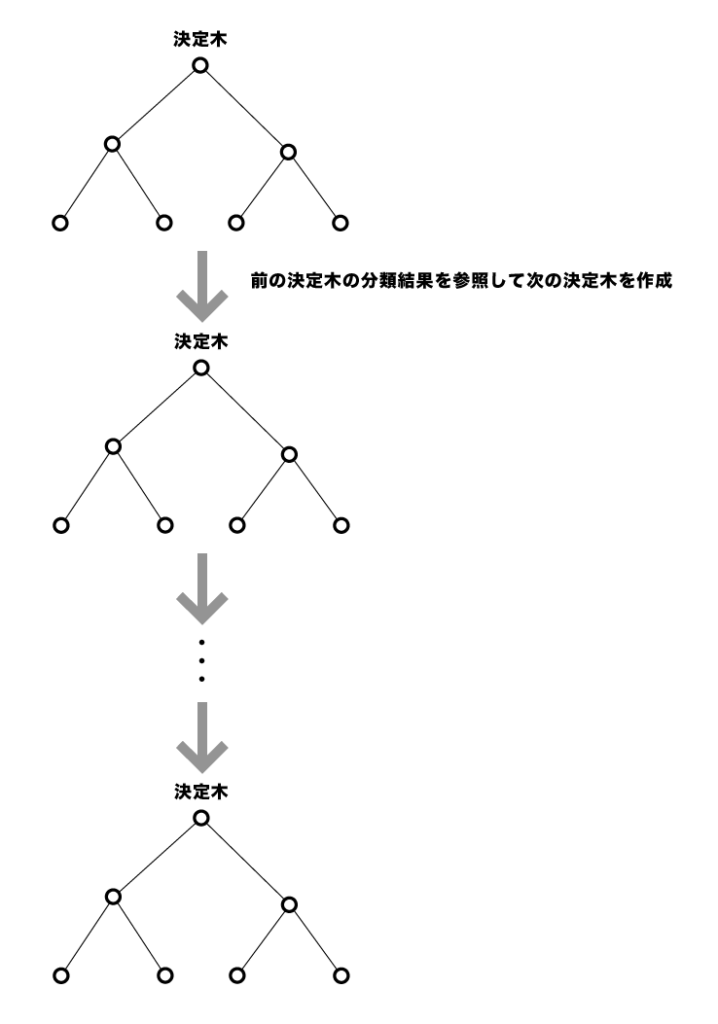
ではightGBMのライブラリをインポートし、ハイパーパラメータを設定します。のちほど調整するため、ここではひとまず回帰分析用のモデルである”objective”を”regression”にだけ設定しておきます。
|
1 2 3 4 5 6 |
import lightgbm as lgb lgbm_params = { 'objective':'regression', 'random_seed':1234 } |
本記事では学習データを3分割し、各データでモデルを作成した際のテストデータに対する予測精度の平均を確認してみます。まずクロスバリデーションするためのライブラリを読み込み、分割数を3と設定しておきます。
|
1 2 3 |
from sklearn.model_selection import KFold folds = 3 kf = KFold(n_splits=folds) |
本コンペの評価指標がRMSEとなるので、その数値を出すためのライブラリもインポートしておきます。
|
1 |
from sklearn.metrics import mean_squared_error |
では各foldごとにmodelsに作成したモデル、rmsesにrmseの計算結果を格納するとともに、oof (out of fold：そのデータ以外を用いて作成したモデルでそのデータの目的変数を予測した値）を保存しておきます。oofは初期値では0の値を入れておき、各foldごとに該当するindexの値を更新していきます。各kf.split（ここでは3つ）で、train_Xを分割した結果のindexが得られますので、そのindexを元に、学習データ、検証データを指定し、LightGBMを実行していきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
train_X = train_df_le.drop(["SalePrice", "Id"], axis=1) train_Y = train_df_le["SalePrice"] models = [] rmses = [] oof = np.zeros(len(train_X)) for train_index, val_index in kf.split(train_X): X_train = train_X.iloc[train_index] X_valid = train_X.iloc[val_index] y_train = train_Y.iloc[train_index] y_valid = train_Y.iloc[val_index] lgb_train = lgb.Dataset(X_train, y_train) lgb_eval = lgb.Dataset(X_valid, y_valid,reference=lgb_train) model_lgb = lgb.train(lgbm_params, lgb_train, valid_sets=lgb_eval, num_boost_round=100, early_stopping_rounds=20, verbose_eval=10, ) y_pred = model_lgb.predict(X_valid, num_iteration=model_lgb.best_iteration) tmp_rmse = np.sqrt(mean_squared_error(np.log(y_valid), np.log(y_pred))) print(tmp_rmse) models.append(model_lgb) rmses.append(tmp_rmse) oof[val_index] = y_pred print(sum(rmses)/len(rmses)) |
上記の結果、平均RMSEは0.1370とまずまずな値になりました。ここから精度を改善していきましょう。
| (3) モデルの改善
まずはここであらためて目的変数の分布を確認してみます。
|
1 |
train_df["SalePrice"].plot.hist(bins=20) |
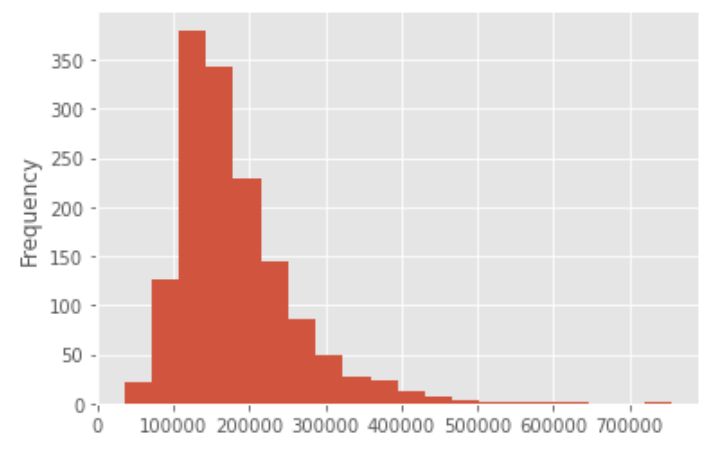
ヒストグラムで確認すると中央値が一番頻度が多く左右対称になっている正規分布と異なり、SalePriceのデータは左側に最頻値が寄っているようです。一般的に、機械学習や統計的な処理の多くはデータが正規分布であることを想定しています。また、感覚的には、16万ドル付近に多くのデータが存在していることから、そこの差異が重要であり、50万ドルか60万ドルかの違いよりも詳細に把握できるようにしていきたいところです。また、本コンペでは評価指標自体が、実際の値の対数と予測値の対数のRMSEとなります。そのため、目的変数を対数化しておいたほうが、評価指標に対して最適化
しやすくなります。Pythonでは以下のようにNumPyを使うことで簡単に対数変換できます。
|
1 |
train_df_le["SalePrice_log"] = np.log(train_df_le["SalePrice"]) |
次に、時間や広さに関する特徴量を追加していきます。例えば、建築年から販売年までの経過年数（築何年か）などです。広さに関するデータは、設備数のデータで割ることで、例えば1つの部屋あたりの広さなどを算出することができそうです。
all_dfをtrain_dfとtest_dfをまとめたもの（pd.concatで連結したもの）としたとき、下記のようにして特徴量を追加することができます。ここでPorchは広さの合計を算出したあと、そもそもPorchがない家が多かったので、ここではPorchの広さの合計をPorchがあるかないかの0、1の値に変換します。変換後は、もとの「Total_PorchSF」は削除しておきます。
|
1 2 3 4 5 6 7 8 |
all_df["Age"] = all_df["YrSold"] - all_df["YearBuilt"] all_df["TotalSF"] = all_df["TotalBsmtSF"] + all_df["1stFlrSF"] + all_df["2ndFlrSF"] all_df["Total_Bathrooms"] = all_df["FullBath"] + all_df["HalfBath"] + all_df["BsmtFullBath"] + all_df["BsmtHalfBath"] all_df["Total_PorchSF"] = all_df["WoodDeckSF"] + all_df["OpenPorchSF"] + all_df["EnclosedPorch"] + all_df["3SsnPorch"] + all_df["ScreenPorch"] all_df['hasPorch'] = all_df['Total_PorchSF'].apply(lambda x: 1 if x > 0 else 0) all_df = all_df.drop("Total_PorchSF",axis=1) |
本記事では割愛しますが、その他、欠損値の処理や外れ値の処理については記事冒頭の全体のnotebookあるいは書籍にて詳細解説しておりますのであわせてご参照くださいませ。
| (4) ハイパーパラメータチューニング
機械学習のモデルにはハイパーパラメータと呼ばれる、挙動を設定するための値があります。ハイパーパラメータは、1つを変更するだけでは精度が向上しないことも多く、複数のハイパーパラメータを同時に変更していくことが必要です。しかし、いくつものハイパーパラメータの値の組み合わせをテストするのは大変です。そこで、Pythonには、様々なハイパーパラメータ最適化用のライブラリがあります。昔からよく使われているグリッドサーチを用いたライブラリや、ベイズ最適化によりグリッドサーチよりも計算量を大幅に改善したものなどがあります。
ベイズ最適化を用いた手法の中でも、近年、PFN（プリファードネットワークス） により開発されたOptunaというライブラリが、効果的なハイパーパラメータを効率的に選択してくれますので、そちらを用いることにします。
まずはターミナルでOptunaをインストールします。
|
1 |
pip install optuna |
次に、Optunaをインポートしたあと、学習データ・検証データを作成し、ハイパーパラメータを最適化します。ここでは、num_leaves、max_bin、bagging_fraction、bagging_freq、feature_fraction、min_data_in_leaf、min_sum_hessian_in_leafを最適化させることにします。なお、LightGBMにおいて調整可能なハイパーパラメータ、初期値、および各値の意味は、LightGBM公式ページにまとめられているのでご参照ください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import optuna from sklearn.model_selection import train_test_split X_train, X_valid, y_train, y_valid = train_test_split(train_X, train_Y, test_size=0.2) def objective(trial): params = { "objective":"regression", "random_seed":1234, "learning_rate":0.05, "n_estimators":1000, "num_leaves":trial.suggest_int("num_leaves",4,64), "max_bin":trial.suggest_int("max_bin",50,200), "bagging_fraction":trial.suggest_uniform("bagging_fraction",0.4,0.9), "bagging_freq":trial.suggest_int("bagging_freq",1,10), "feature_fraction":trial.suggest_uniform("feature_fraction",0.4,0.9), "min_data_in_leaf":trial.suggest_int("min_data_in_leaf",2,16), "min_sum_hessian_in_leaf":trial.suggest_int("min_sum_hessian_in_leaf",1,10), } lgb_train = lgb.Dataset(X_train, y_train) lgb_eval = lgb.Dataset(X_valid, y_valid, reference=lgb_train) model_lgb = lgb.train(params, lgb_train, valid_sets=lgb_eval, num_boost_round=100, early_stopping_rounds=20, verbose_eval=10,) y_pred = model_lgb.predict(X_valid, num_iteration=model_lgb.best_iteration) score = np.sqrt(mean_squared_error(y_valid, y_pred)) return score study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=0)) study.optimize(objective, n_trials=50) study.best_params |
上記を実行すると例えば下記のようにOptunaで最適化されたハイパーパラメータを得ることができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
lgbm_params = { "objective":"regression", "num_leaves":34, "learning_rate":0.05, "n_estimators":1000, "max_bin":109, "bagging_fraction":0.6922380344778845, "bagging_freq":4, "feature_fraction":0.5460737633962744, "min_data_in_leaf":12, "min_sum_hessian_in_leaf":10 } |
| (5) 複数手法のアンサンブル
続いては、LightGBMと同じGradient Boosting Decision Treeの実装であるXGBoostを試してみます。XGBoostは、非常に精度が高く、予測タスクにおいて重宝されていたのですが、実行速度でLightGBMが勝ることで、近年の予測タスクではLightGBMが広く使用されているように思います。ただし、XGBoostも、LightGBMを用いた学習で特徴量生成や前処理が終わった後に、最後の予測結果の組み合わせに活用されることが多い印象です。
まずはターミナルでXGBoostをインストールします。
|
1 |
pip install xgboost |
実装はLightGBMと似ているのですが、category変数を読み込むことはできないため、int型に変換しておきます。
|
1 2 3 4 |
categories = train_X.columns[train_X.dtypes == "category"] for col in categories: train_X[col] = train_X[col].astype("int8") test_X[col] = test_X[col].astype("int8") |
XGBoostでも前述のOptunaで最適化されたハイパーパラメータを取得しておきましょう。そのパラメータをxgb_paramsとして記載したのち下記のようにして実行できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import xgboost as xgb models_xgb = [] rmses_xgb = [] oof_xgb = np.zeros(len(train_X)) for train_index, val_index in kf.split(train_X): X_train = train_X.iloc[train_index] X_valid = train_X.iloc[val_index] y_train = train_Y.iloc[train_index] y_valid = train_Y.iloc[val_index] xgb_train = xgb.DMatrix(X_train, label=y_train) xgb_eval = xgb.DMatrix(X_valid, label=y_valid) evals = [(xgb_train, "train"), (xgb_eval, "eval")] model_xgb = xgb.train(xgb_params, xgb_train, evals=evals, num_boost_round=1000, early_stopping_rounds=20, verbose_eval=20,) y_pred = model_xgb.predict(xgb_eval) tmp_rmse = np.sqrt(mean_squared_error(y_valid, y_pred)) print(tmp_rmse) models_xgb.append(model_xgb) rmses_xgb.append(tmp_rmse) oof_xgb[val_index] = y_pred xgb_test = xgb.DMatrix(test_X) preds_xgb = [] for model in models_xgb: pred = model.predict(xgb_test) preds_xgb.append(pred) preds_array_xgb= np.array(preds_xgb) preds_mean_xgb = np.mean(preds_array_xgb, axis=0) preds_exp_xgb = np.exp(preds_mean_xgb) submission["SalePrice"] = preds_exp_xgb |
上記の結果、XGBoostの予測結果も得ることができます。最後にXGBoostとLightGBMの結果を組み合わせてみます。様々な予測モデルを組み合わせて1つの（メタ）モデルとする手法をアンサンブルと言います。複数のモデルを用意し、各モデルの予測結果の多数決をすることで、単体のモデルよりも精度向上を狙うというものです。理論の詳細は本書では割愛しますが、直感的な理解のための説明をしますと、ランダムに結果を返すよりも精度の高いモデルが複数あった時、お互いのモデルが十分に独立しているならば、その複数のモデルの予測がすべて間違える確率はとても低いということがアンサンブルの精度がよい理由になります。
ここでは試しにXGBoostの予測結果とLightGBMの予測結果をそれぞれ0.5ずつの重みで組み合わせる、つまり平均をとることにします。
|
1 2 |
preds_ans = preds_exp_xgb * 0.5 + preds_exp * 0.5 submission["SalePrice"] = preds_ans |
以上のようにして最終的なアンサンブルした予測結果を得ることができました。本記事以外の前処理も加えたもので実際にKaggleに投稿してみると「0.12689」という予測精度の結果となりました。本記事で省略した箇所含め全体コードのnotebook、その解説は下記の書籍を参照くださいませ。
本記事のコード/ご参照
・本記事の全体のコードのnotebookを以下にアップしております。あわせてご参照くださいませ。
“Kaggle houseprices-tutorial-code”
・本記事含むKaggleやデータ分析初学者向けのチュートリアル解説本を執筆しました。あわせてご参照くださいませ。 ※本記事のコードや環境構築の詳細手順を記載した書籍となります。
『Pythonで動かして学ぶ！Kaggleデータ分析入門』
・本記事の全体のコードのnotebookを以下にアップしております。あわせてご参照くださいませ。
“Kaggle houseprices-tutorial-code”
・本記事含むKaggleやデータ分析初学者向けのチュートリアル解説本を執筆しました。あわせてご参照くださいませ。 ※本記事のコードや環境構築の詳細手順を記載した書籍となります。
『Pythonで動かして学ぶ！Kaggleデータ分析入門』
関連記事:
人気記事:
