日本全国各所で猛暑日が続き、
facebookは野外フェスと海と海外旅行とビアガーデンの写真が溢れ始めております。
しかし猛暑だろうが極寒だろうが、
データ分析官は、週末のビールを信じて
黙々とパソコンに向き合う日々なはずです。
ところが、この週末ビールを阻む大いなる壁があります。
そう、もうお気づきかと思いますが、みなさんおなじみ”既読スルー”です。
飲みに誘ってもレスポンスが無いのですから飲みに行けません。(一人飲みをするには勇気が足りない)
「え?既読スルーて、友人の間でもカジュアルに起こる事なの?」と思った貴君、
私だってこの状態が当たり前だとは思っておりません。
メールコミュニケーションの時代は、返信が来なかろうが
「もう寝たんだろう」「海外旅行中なんだろう」「ケータイ紛失したんだろう」
「深爪してメールを打つのも困難なんだろう」などと、
あり得ないほどのオプティミストな思考が思春期を生き残る必須のスキルの1つでした。
今のチャットアプリの時代では「既読」がありますので、そうはいきません。
前置きが長くなりましたが、本稿では、
「LINEのやりとりデータをランダムフォレストを用いて機械学習し、
“返信”と”既読スルー”の予測モデルを構築」します。
これによって、オプティミストな思考をしなくとも、
「木曜日20時以降で、松村さんに対して飲みの用事で送ったのであれば78%返信が来なくても当然」
と論理的に判断する事ができ、もう一歩踏み込むと、既読スルーされないためには、
何曜日何時、誰に、どのようなトピックでLINEするべきか、がわかります。
以下が今回分析に用いた私の直近のLINEデータとなります。
※本物のデータを用いないと(私のプライベートにとって)意味がありませんので、そのままのデータです。
相手の名前のみ偽名です。
※LINEデータの取得方法は過去エントリー「LINEのトーク履歴を取得する。」を参照くださいませ。
※ローデータから、各種前処理・分類をしてパラメータを生成しております。
※やり取りが発生以降は、連続したセッションとしてまとめております。
相手から最初のレスポンスがあるまでのやりとりのみ抽出しております。
※機械学習で分析するには心もとないデータ数ですが、つべこべ言ってられません。
変数は以下の通りです。
| week | 曜日 |
| time | 送信時間 |
| topic | drink(飲み)、play(遊び)、question(質問)、 birthday(誕生日祝)、information(情報共有)の5種 |
| to | 送信相手 |
| length | 文字数 |
| result | yes(24時間以内に返信あり) no(24時間以内に返信無し) |
得られたデータは下記となります。
| week | time | topic | to | length | result |
| tue | 22 | drink | sasaki | 8 | no |
| fri | 23 | drink | sasaki | 12 | no |
| fri | 14 | drink | sasaki | 15 | yes |
| sat | 12 | drink | sasaki | 11 | yes |
| sat | 15 | drink | sasaki | 19 | yes |
| sat | 15 | drink | sasaki | 57 | yes |
| sat | 18 | drink | sasaki | 16 | yes |
| sat | 19 | drink | sasaki | 13 | yes |
| sun | 19 | play | sasaki | 25 | yes |
| tue | 11 | play | sasaki | 17 | yes |
| mon | 9 | play | sasaki | 36 | no |
| sun | 16 | question | matsuda | 9 | yes |
| fri | 17 | play | matsuda | 19 | yes |
| wed | 9 | play | konishi | 29 | yes |
| wed | 23 | play | konishi | 36 | no |
| fri | 8 | play | konishi | 44 | yes |
| sat | 22 | drink | satomura | 24 | yes |
| fri | 22 | play | satomura | 65 | yes |
| sat | 0 | birthday | hirata | 54 | yes |
| tue | 11 | question | hirata | 75 | yes |
| fri | 10 | drink | hirata | 183 | no |
| mon | 11 | drink | kuwano | 60 | no |
| wed | 21 | play | kuwano | 63 | no |
| sat | 13 | play | kuwano | 30 | yes |
| sat | 12 | play | kuwano | 44 | no |
| sun | 1 | play | kuwano | 40 | yes |
| mon | 3 | information | sato | 105 | yes |
| sat | 20 | drink | sato | 185 | no |
| tue | 15 | drink | sato | 100 | no |
| wed | 22 | drink | sato | 86 | no |
| wed | 2 | drink | sato | 133 | no |
| mon | 11 | information | sato | 350 | yes |
| wed | 12 | information | sato | 395 | yes |
| thu | 21 | drink | sato | 165 | yes |
| sat | 12 | drink | sato | 17 | yes |
| sun | 12 | drink | sato | 45 | yes |
| sat | 10 | information | hashimoto | 187 | no |
| sat | 19 | drink | hashimoto | 72 | yes |
| thu | 18 | drink | hashimoto | 44 | yes |
| fri | 13 | drink | hashimoto | 71 | yes |
| thu | 9 | drink | hashimoto | 161 | yes |
| thu | 12 | drink | fujimoto | 277 | yes |
| wed | 18 | information | saito | 74 | no |
| tue | 10 | drink | matsumura | 67 | no |
| sun | 4 | drink | matsumura | 83 | no |
| thu | 22 | drink | matsumura | 20 | no |
| sat | 19 | drink | matsumura | 43 | yes |
| thu | 19 | drink | matsumura | 55 | yes |
| mon | 12 | information | matsumura | 89 | no |
| fri | 8 | question | murata | 165 | yes |
| sat | 18 | drink | murata | 124 | yes |
まずは、上記データをRに取り込み、データ分析する前に、可視化してデータ探索してみます。
おなじみggplotを使っていきましょう。
|
1 |
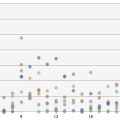
ggplot(data=df,aes(x=week,y=time))+geom_point(aes(colour=result))+ scale_y_reverse() |
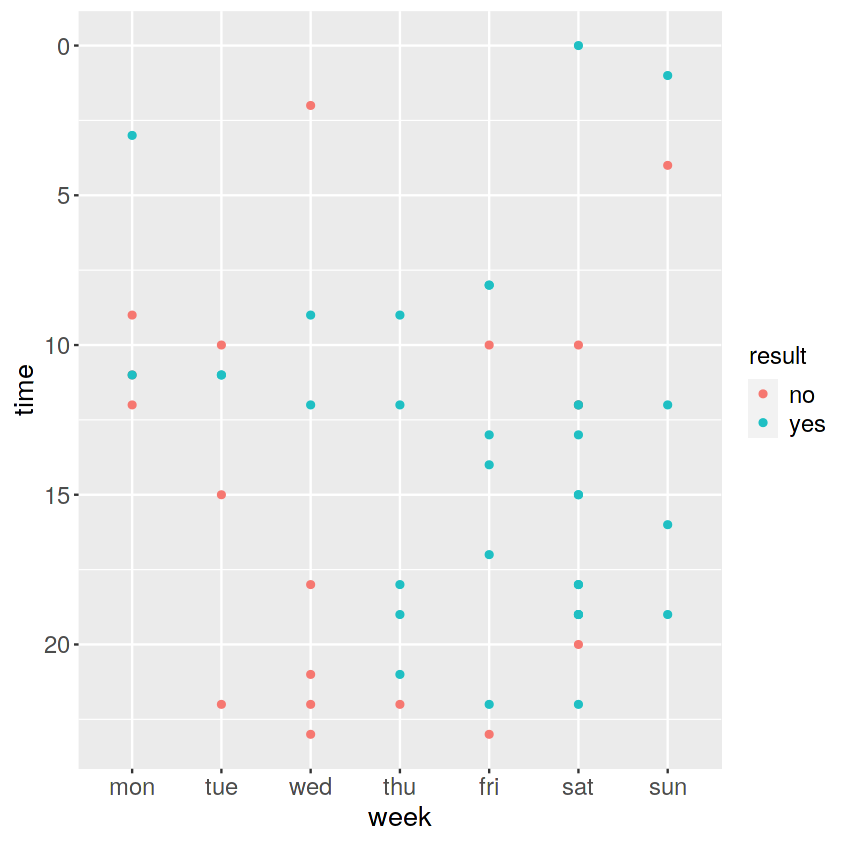
縦軸が送信曜日、横軸が送信時間、
凡例は、緑色が「返信あり」、赤色が「返信なし」です。
本来ヒートマップなどで確認したいところですが、
今回はデータが少ないので、散布図でプロットしております。
次に、送信時間と送信相手を見てみましょう。
|
1 |
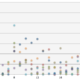
ggplot(data=private_mail,aes(x=to,y=time))+geom_point(aes(colour=result)) |
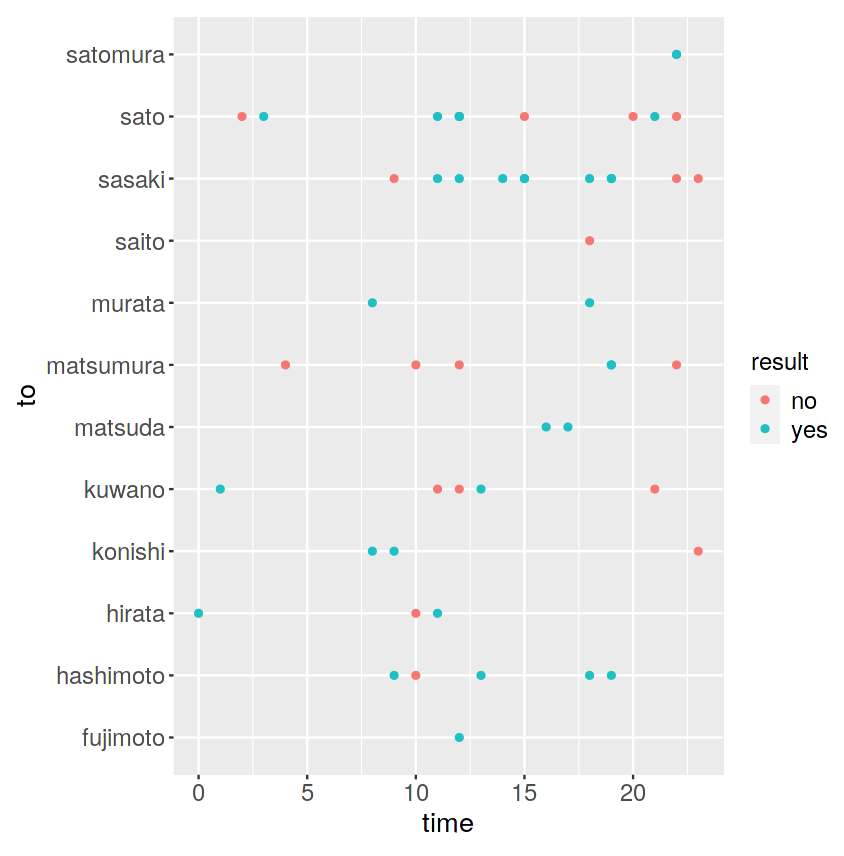
今度は縦軸がLINEの送信先の相手、横軸が送信時間、
凡例は、緑色が「返信あり」、赤色が「返信なし」です。
fujimotoさん、matsudaさん、murataさん、satomuraさん、とは
正常なコミュニケーションがとれているようです。
matsumuraさん、ほぼ返信がありませんが、どういうことでしょうか。
最後に、縦軸が送信時間、横軸が文字数、
凡例は、緑色が「返信あり」、赤色が「返信なし」です。
|
1 |
ggplot(data=private_mail,aes(x=length,y=time))+geom_point(aes(colour=result)) |
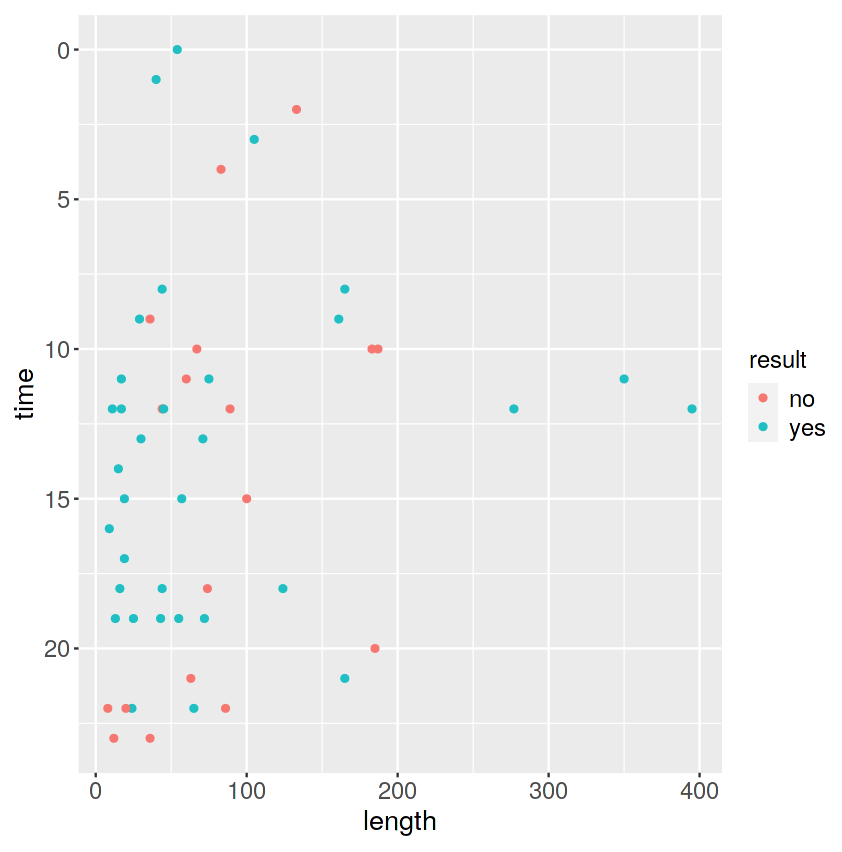
文字数が長いLINEは返信があるようで何よりです。
とはいえ、200文字近いLINEを送って既読スルーされたときもあるようです。
これは送る方も、送られた方も、辛いです。
さて、ではこのデータを解析していきましょう。
今回はランダムフォレストを用いようと思います。
ランダムフォレストは決定木の応用となります。
なお決定木は、ジニ係数などの分岐基準を用いて、
最も結果を分けるのにふさわしいパラメータを選択し続けていくものです。
なぜ、決定木では充分ではないのでしょうか。
そこで、ランダムフォレストの簡単な説明もかねて、
まずは決定木で本データを解析してみましょう。
|
1 2 3 4 |
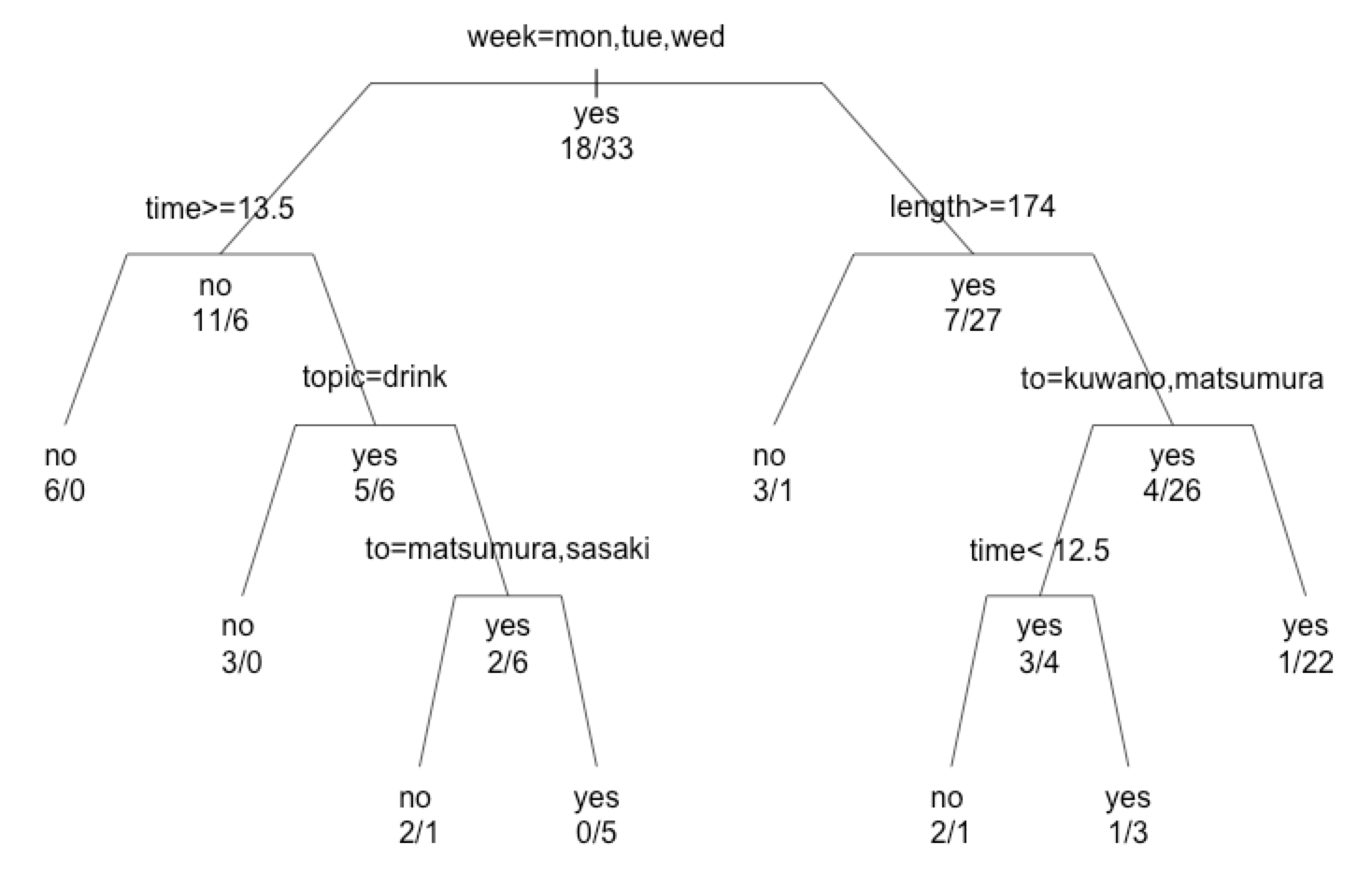
library(rpart) mail.rp <- rpart(result~.,private_mail) plot(mail.rp,margin=0.1,uniform=T) text(mail.rp,all=T,use.n=T,pretty=0) |
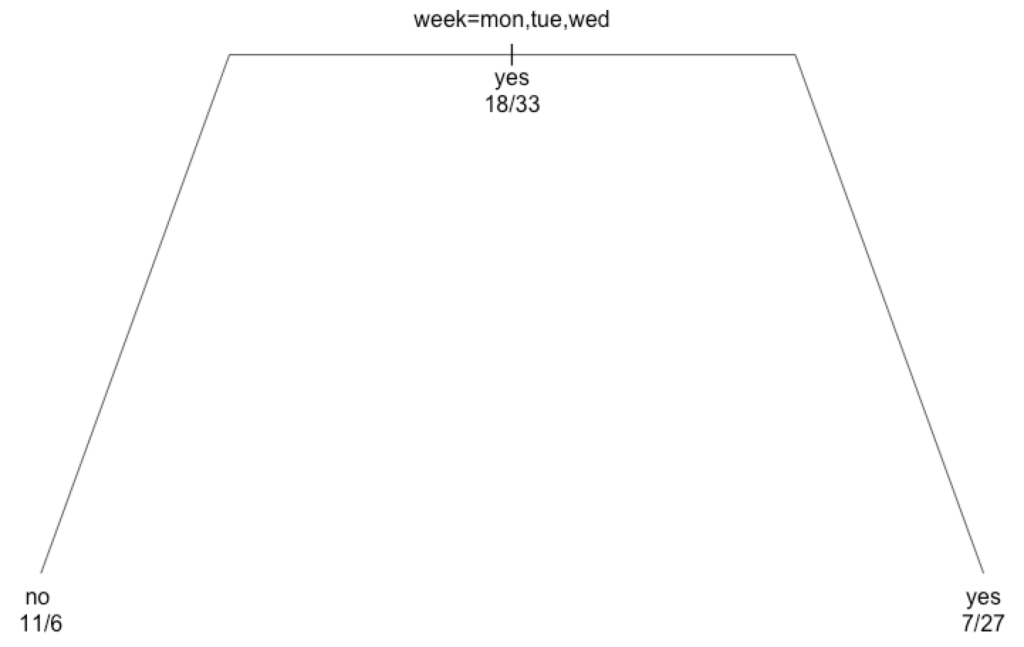
「曜日で分類して、”月”・”火”・”水”に送ると返信来ないことのほうが多いから、
木曜日以降のほうがいい」という結果です。
データ分析官にデータ依頼して1週間待って出てきたのがこれだけだと震えますよね。
もっと他にいろんな要素とか無いものだろうか、とお思いかと思います。
そこで、決定木では、「繁らせる(分岐を増やす)」ことと「プルーニング(分岐を減らす)」を
適宜行っていく事で、精度および実用性を上げていきます。
R上では、controlとして指定します。
木の複雑さを表すcpが、経験上デフォルトだと厳しいと思いますので、少し緩めてみます。
|
1 |
mail.rp <- rpart(result~., data=private_mail, control=rpart.control(minsplit=5, cp=0.01)) |
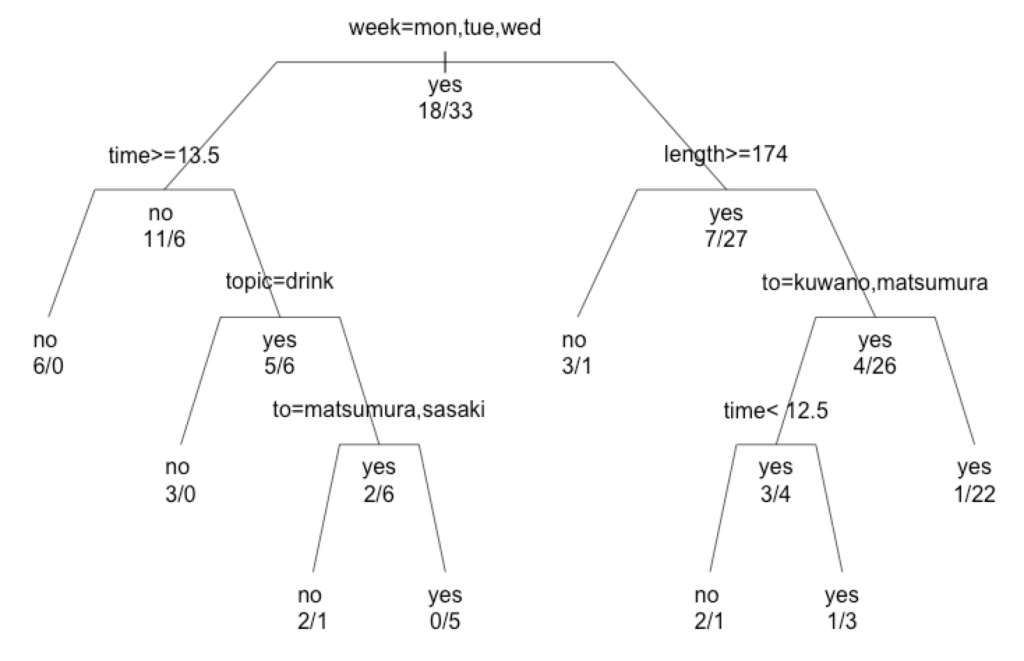
分岐上限が増え、決定木らしくなりました。
上記のようなcpをどの程度にしたら良いかは、別途方法があるのですが、
今回は決定木はここまでにしておきます。
さて、このようにして得られる決定木は解釈が容易な反面、
必ずしも最適なパラメータが選択されるとは限らない、という欠点があります。
たとえば、異常値や影響の大きいパラメータの存在などによって、
最初の分岐が(最適なものではなく)決まると以降の分岐は、その前提で進んでいくことになります。
そこで、全てのパラメータを用いるのではなく、任意のパラメータを部分的にランダムに選択してきて、
そこから決定木を作る、ということを複数回行うことで、
一部のパラメータのみに引っ張られることが無いようにし、
その複数の決定木の結果を多数決(ないしは平均値)で予測するという考えが
ランダムフォレスト、となります。
R上では非常にシンプルに下記で実行できます。
|
1 2 3 |
library(randomForest) mail.rf<-randomForest(result~.,data=private_mail) mail.rf |
本データでは下記の結果となりました。
Call:
randomForest(formula = result ~ ., data = private_mail)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 43.14%
Confusion matrix:
no yes class.error
no 4 14 0.7777778
yes 8 25 0.2424242
| no | yes | class.error | |
| no | 4 | 14 | 0.77 |
| yes | 8 | 25 | 0.24 |
yesもnoのときも、どちらもyesと予測してしまっている数が多いようです。
ちなみに現時点でのエラー率は43.14%のようです。
まずは今回、yes=33、no=18と不均衡データとなっておりますので、
重みをつけて調整することにしましょう。
また、ランダムフォレストは、全パラメータの中からどれだけの数を各決定木で選択するかを、
“mtry”、という値で調整することが出来ます。
tuneRFというコマンドを用いることで、自動的に最適なmtryパラメータを探索できます。
最初にパラメータ、次に目的変数を記入します。
※6行目が目的変数で、それ以外が説明変数、yesとnoの数が33:18で逆に重みをかけて調整するときは下記。
|
1 |
mail.tune<-tuneRF(private_mail[,-6],private_mail[,6],doBest=T,classwt=c(18,33)) |
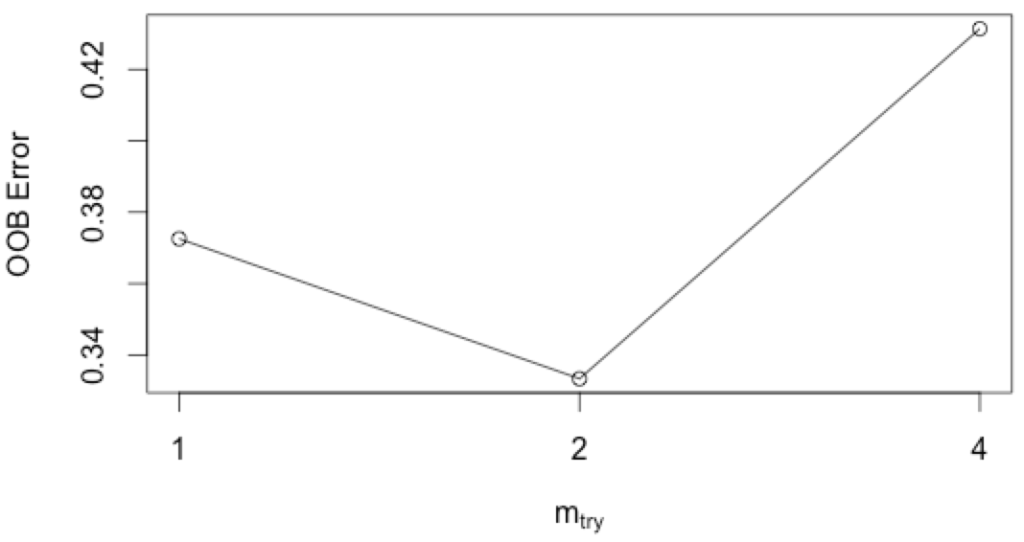
縦軸がエラー率ですので、各決定木に使うパラメータ数は2が良いようなので、mtry=2とします。
ではもう一度実行してみましょう。ちなみに作成する決定木の数もntreeで指定する事が出来ます。
この数が少ないと毎回結果がブレますので、大きめに2000としておきましょう。
まとめると下記となります。
|
1 2 3 |
library(randomForest) mail.rf<-randomForest(result~.,data=private_mail,mtry=2,ntree=2000,weight=c(18,33)) mail.rf |
Call:
randomForest(formula = result ~ ., data = private_mail, mtry = 2, weight = c(18, 33), ntree = 2000)
Type of random forest: classification
Number of trees: 2000
No. of variables tried at each split: 2
OOB estimate of error rate: 37.25%
Confusion matrix:
no yes class.error
no 4 14 0.7777778
yes 5 28 0.1515152
| no | yes | class.error | |
| no | 4 | 14 | 0.77 |
| yes | 5 | 28 | 0.15 |
エラー率は37.25%に改善されました。
yesの時にnoと予測する点が改善されたようです。
本当は、noのときにyesと予測してしまう点を改善したかったのですが。
(返信が来るときでも来ないと予測する機会損失よりも、
返信が来ないのに来ると予測するリスクを改善したかった。
いえ、ある意味、一歩踏み出すためのポジティブな予測モデルとして、
これでよいのかもしれません。)
最後にこのモデルで計算された各変数の重要度(ジニ係数)を下記のようにして算出しておきます。
|
1 |
importance(mail.rf) |
| variable | MeanDecreaseGini |
| week | 5.235269 |
| time | 5.070753 |
| topic | 1.697444 |
| to | 5.415680 |
| length | 5.221605 |
もしパラメータが多いデータの場合は、上記をもとに、
パラメータを重要なものに絞ることが出来ます。
※パラメータを重要なものに絞るためにランダムフォレストを前処理として行い、
以降を別の処理にかけることも考えられます。
さて、以上で予測モデルは完成となります。
LINEの返答率の結果ですが、
「誰に出すか」が最も重要で、次に「曜日」が影響あるようです。
※あくまで私個人のLINE履歴の傾向であることに留意くださいませ。
作成されたモデルに、新たなデータを入力として用いれば、その入力の結果を予測出来ます。
さてこれで、LINEの通知が来るたびに、少しの淡い期待でアプリを見たときに、
LINEを送ったはずの松村さんからの返信ではなく母親からだったときのやるせない思いとは無縁になるはずです。
晴れて多くの友人と飲み会に行けることでしょう。
しかし飲み会は飲み会で孤立の罠があります。
念の為、過去エントリー「飲み会で孤立しないためのセルオートマトン」を
参照いただければと思います。