12月の忘年会が終われば1月の新年会、
3月の解散会、4月のキックオフ会、など、
社会人は年末年始から春にかけては、特に飲む機会が多いように思います。
さらに土日にも、結婚式の2次会などがある方もいることでしょう。
さて、ここで重要なことは、“いかにして孤立しないか”、となります。
しかし、従来、多くの場合においてそれはコミュニケーション上の問題と誤解されておりました。
プログラマであれば、
それはコミュニケーション上の課題ではなく、プログラミングで解決するべき課題である、
と認識すべきかと思います。
飲み会における、前提条件は多くの場合、下記のとおり整理できます。
・他の参加者のうち、自分と親しい人の位置が重要である。
・親しい人が周りに多ければ孤立しないが拡がりは無い。
・しかし親しくない人に囲まれると孤立する。
・ある程度親しい人が周りにいるときのみ、親しくなかった人とも親しくなり交流できる。
お気づきの通り、これはまさに、セル・オートマトンで解決できる問題となります。
※正確に言うと、セル・オートマトンの変形
セル・オートマトンとは、近傍のセルの状態の影響を考慮する、
時系列の状態遷移を扱うシミュレーションモデルとなります。
簡単に1次元のセル・オートマトンを例にして見ていきます。
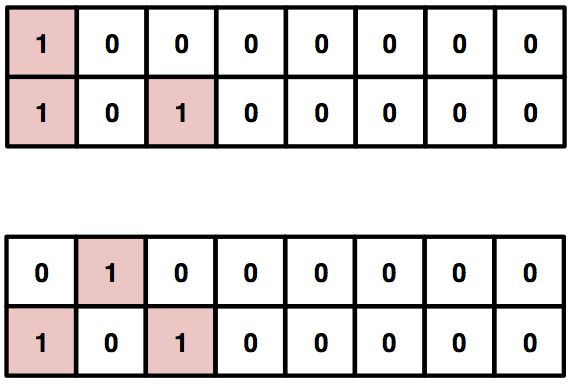
時刻tにおける下記のような配列、および”状態”があったとします。
(“状態”とは、”0″か”1″の値を考えます。たとえば”白”か”黒”、”生”か”死”か、などです。)
![]()
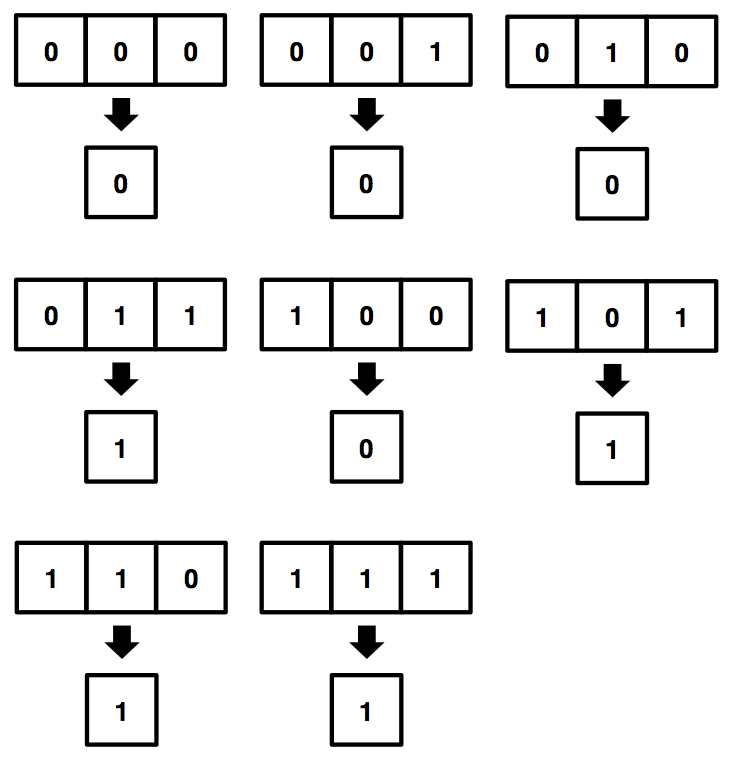
次に各セルにおいて、自分と近傍(ここでは左右1つ隣)の状態をもとにした、
状態遷移のルールを決めておきます。
たとえば適当に下記のようなルールを考えましょう。
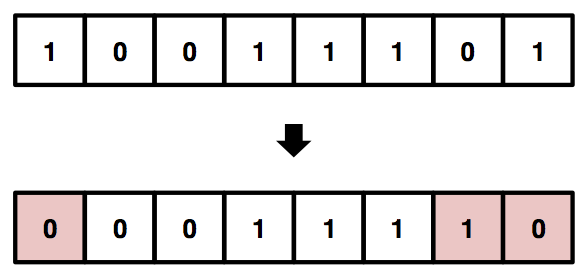
すると、上記時刻tの状態、状態遷移のルールから、時刻t+1の状態は、
下記のとおりになります。
※すべてのセルにおいてルールが適用。左右端のセルは、一定の値(ここでは”0″)とする。
※状態がルールによって変化したもののみ、色付け。
さらにこれに状態遷移のルールから時刻t+2の状態をつくり、、といった手順で
シミュレーションを進めていきます。
その概念は1940年代にロスアラモス国立研究所で
スタニスワフ・ウラムとジョン・フォン・ノイマンによって発見されました。
おそらくウラムとフォン・ノイマンも”飲み会での孤立”、という悩みを持っていたのではないでしょうか。
さて、このセル・オートマトンを今回の飲み会シミュレーションに取り入れるには、
1つ大きな変形が必要です。
それは”自分”と”友人”という、状態不変の概念を入れることです。
そうでないと、”盛り上がっている人”、”盛り上がっていない人”の2つの状態をもつ、
飲み会の盛り上がりのシミュレーション、となってしまいます。(それはそれで面白そうですが)
では、前置きが長くなりましたが、以下2パターンで、
“飲み会での孤立脱却のためのシミュレーションモデル”を見ていきましょう。
(1) 中小規模の着席型の飲み会の場合
この場合、前提条件は下記の通りとなります。
・席は一定時間固定で移動しない。
・20人の部内で、親しい人が2人は存在し、それ以外の人とは話したことがない。
・親しい人が近くに1人いても話題は広がらないが、2人以上いると、他の人も含め話が広がり、
話したことが無い人とも話せるようになる。(親しい人になる)
・ただし、知り合いが3人以上いると、自分以外の人の話がメインになり、
その場での一時的な親しさは失われる。
・自分が近傍にいなくても(席を離れていても)、
自分と親しい人が集まれば、自然発生的に自分の話になる可能性があり、自分もその話題に入れる。
言うまでもなく、いかに最初の着席配置をどうするか、にすべてがかかっています。
いくつかのシミュレーション結果を見てみましょう。
まず、初心者がやってしまいがちな、仲のいい人で固まるというパターン。
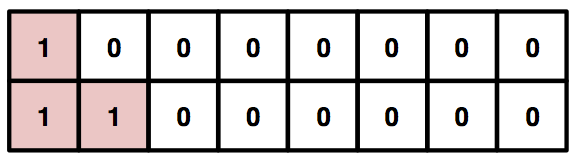
これは、早々に話題がなくなって詰みます。
※セル・オートマトン的には、数ターン以内にすべて”0″になる。
では、どうするべきか。
ひとつ席を外して固めるのです。
例えば下記のような状態です。
こうすることで話題をつなぎつつも、新しい人とも仲良くなれます。
※セル・オートマトンの実際のある時点でのシミュレーションキャプチャ(processingで実装)。
自分は赤、
白が”0″、つまりコミュニケーションがとれていない状態。
色(黒が”1″、赤、青がそのターンで色が変わったもの)がついているものが、コミュニケーションが発生している状態。
うまくコミュニケーションが発生しております。
![]()
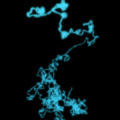
(2) 大規模な立食型の飲み会の場合
続いてもう少し複雑な状況を考えます。
この場合、前提条件は下記の通りとなります。
・任意の時間ごとに、”自分”は移動できる。
・100人の立席者で、親しい人が5,6人は存在し、それ以外の人とは話したことがない。
・親しい人が近くに1人いても話題は広がらないが、2人以上いると、他の人も含め話が広がり、
話したことが無い人とも話せるようになる。
・ただし、知り合いが3人以上いると、自分以外の人の話がメインになり、
その場での一時的な親しさは失われる。
・自分が近傍にいなければ、自分の話題になることはない。(状態が”0″になる)
こちらは、自分の親しい人がどのように分散しているかを序盤で見極めて、
いかに巧みに移動していくかがポイントです。
とにかく、一カ所にとどまらないことです。
たとえ友人が一カ所に固まっている場合でも、ポジションを巧みに変えるとよいでしょう。
以下シミュレーション結果を見ていただいたほうがわかりやすいかと思います。
赤色が”自分”、青色が”友達”、
それ以外が見知らぬ人ですがコミュニケーションが発生したタイミングで色が変わります。
うまくコミュニケーションが発生している3パターンの友人配置および自分の移動履歴を10秒づつキャプチャしております。
いかがでしたでしょうか。
もはやセル・オートマトンから逸脱していますね。
くれぐれもセル・オートマトンを誤解されないよう、
本来のセル・オートマトンの応用についてはネットで論文などご参照くださいませ。