いよいよ3月にJ1が開幕します。
今年もマリノスは、目立った補強は無く、昨年までの得点力不足は解消されるのか、やきもきしておりましたが、
それに加えて絶対的司令塔の俊輔が手術で開幕には間に合わないようで、
もはやトム・クルーズ抜きでミッションインポッシブルを作るくらいミッションインポッシブルです。
さて、こうなってきますと、ファンとしましては、
シーズン中、どれくらいのゴール数を期待できるのか、
ある程度、心の準備をしておきたく思います。
以前のポストで「横浜F・マリノスの2014年全ゴールをアトリビューション分析」しましたが、
今回は、マリノスの2014年のJ1全試合のゴールおよび、その他の指標を用いて、
ポワソン分布でゴール数をモデリングし、AICでモデル選択する事をやってみます。
ポワソン分布とは、平均値のみで決定される分布でして、
有限のカウントデータを表す事に向いております。
正規分布のような左右対称ではなく、「カウントが多いことは滅多に起こらない」ような表現となります。
たとえば下記のようなものです。
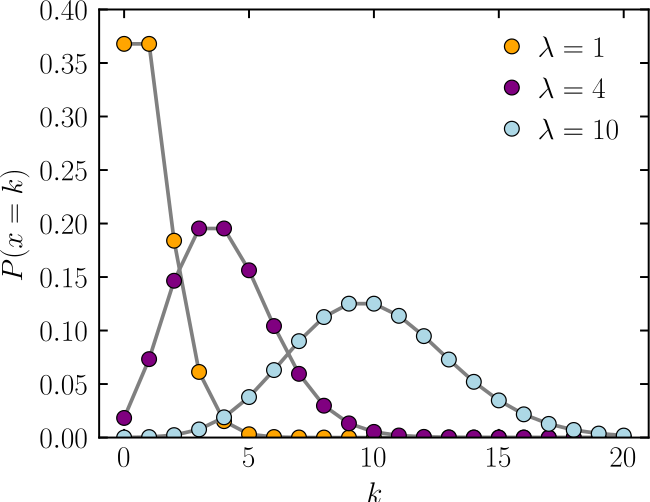
※wikipediaより
ゴールに効きそうな変数として、
特にマリノスはセットプレーが強いチームですので
shooot(シュート数)のほか、CK(コーナーキック)、FK(フリーキック)、などが考えられます。
その他、「home(ホーム/アウェイ)」なども影響があるかもしれません。
さらに「shunsuke(中村俊輔の出場時間)」も考慮してみます。
以上より、データを下記のように用意しました。
【横浜F・マリノスの2014年のJ1全試合のゴールデータ】
※マリノスのホームページの試合データから独自集計
| goal | shunsuke | home | shoot | CK | FK |
| 1 | 36 | away | 5 | 2 | 12 |
| 1 | 24 | home | 11 | 6 | 14 |
| 2 | 13 | away | 10 | 5 | 14 |
| 0 | 20 | home | 12 | 4 | 16 |
| 0 | 90 | home | 11 | 1 | 21 |
| 3 | 90 | away | 10 | 5 | 8 |
| 1 | 90 | home | 15 | 5 | 14 |
| 0 | 0 | away | 11 | 5 | 15 |
| 0 | 0 | home | 6 | 5 | 11 |
| 1 | 46 | home | 9 | 2 | 13 |
| 0 | 90 | away | 1 | 2 | 12 |
| 0 | 90 | home | 9 | 3 | 12 |
| 2 | 90 | away | 14 | 3 | 15 |
| 2 | 90 | home | 17 | 4 | 11 |
| 3 | 87 | away | 10 | 3 | 12 |
| 2 | 64 | home | 15 | 8 | 12 |
| 0 | 90 | away | 8 | 5 | 17 |
| 1 | 90 | away | 10 | 7 | 9 |
| 1 | 90 | home | 16 | 9 | 13 |
| 2 | 90 | away | 14 | 2 | 15 |
| 2 | 90 | away | 9 | 4 | 11 |
| 3 | 90 | away | 12 | 5 | 10 |
| 1 | 44 | home | 13 | 12 | 15 |
| 2 | 52 | home | 9 | 2 | 10 |
| 0 | 90 | away | 8 | 1 | 14 |
| 0 | 90 | home | 10 | 4 | 16 |
| 0 | 90 | away | 8 | 4 | 15 |
| 0 | 90 | home | 11 | 8 | 11 |
| 0 | 90 | away | 12 | 5 | 18 |
| 1 | 90 | home | 6 | 6 | 22 |
| 0 | 90 | away | 4 | 3 | 11 |
| 3 | 90 | home | 13 | 10 | 15 |
| 1 | 90 | away | 10 | 6 | 16 |
| 2 | 90 | home | 14 | 3 | 14 |
まずはデータをいろんな切り口でグラフにしながら眺めてみます。
ちなみにRのグラフは、ggplot2を用いると、デフォルトのグラフと比較して
50万円のエステを受けた後にプロのスタイリストが化粧をし、
さらにphotoshopで原型がなくなるまで加工したくらいきれいに描画されます。
というのは冗談にしても、Rでのグラフの書き方はggplot2で覚えたほうがよいかと思いますので、
以下、ggplot2での描画の仕方を紹介していきます。
今回、ゴール数のモデリングが分析の目的となりますので
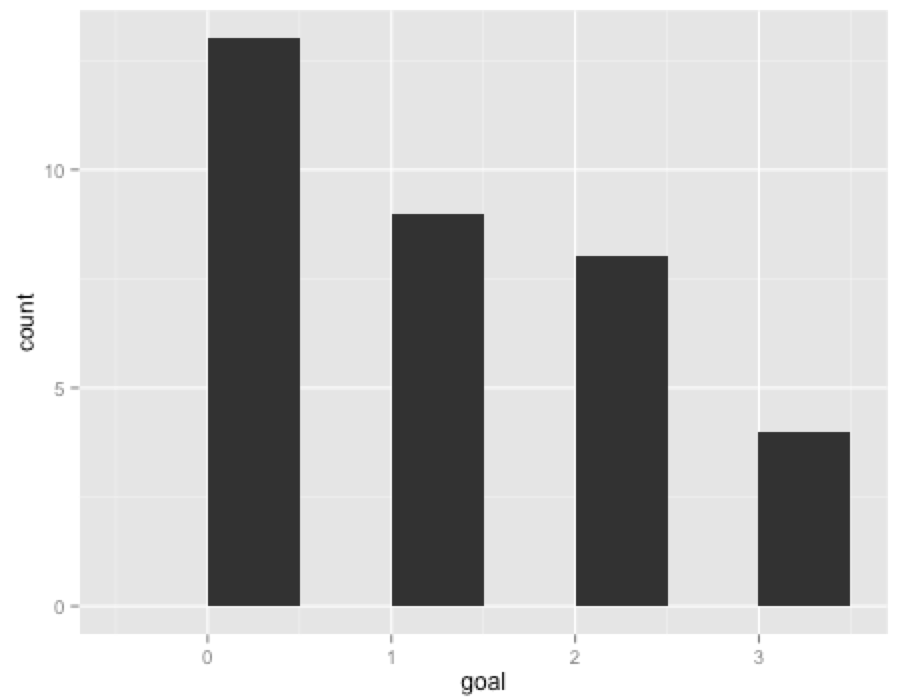
まずは、ゴール数をヒストグラムにしてみます。
|
1 2 3 |
g<-ggplot(marinosu,aes(x=goal)) g<-g+histogram(binwidth=0.5) plot(g) |
残念ながら0点の試合が最も多く、平均ゴール数は1.08となります。
これをhome/awayで切り分けてみたヒストグラムは下記となります。
|
1 2 3 4 5 |
df<-melt(marinosu,id="home") df2<-subset(df,variable=="goal") g<-ggplot(df2,aes(x=value,fill=home)) g<-g + geom_histogram(alpha=0.5,position="dodge",binwidth=0.5) plot(g) |
※meltは、指定した変数ごとにデータが集計される
※geom_histgramはpositionで描画の仕方を指定(dodgeは横に並べて描画)
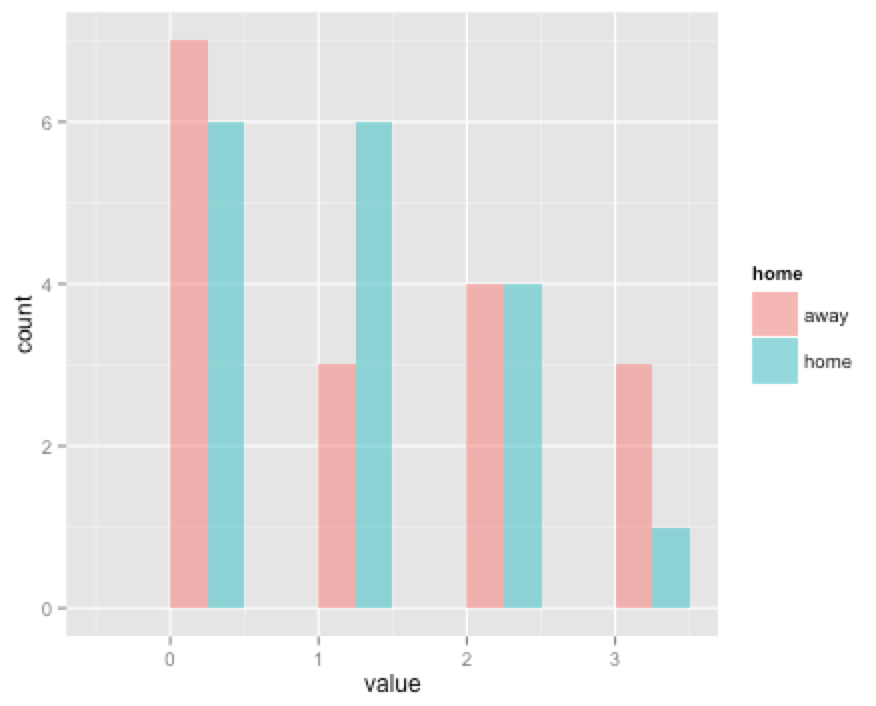
※横軸がゴール数、縦軸がカウント数(そのゴール数が起きた試合数)。
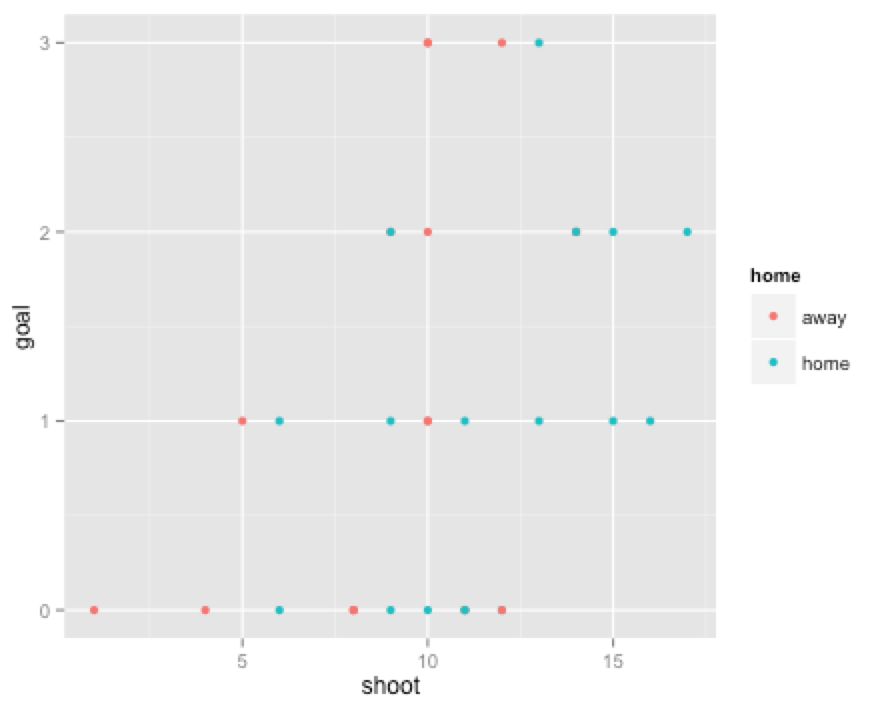
やはり、homeの方が得点しやすいようですが、3点ゴールした試合はawayの方が多いようです。
これは対戦相手(下位チームとのawayゲーム)によるものかもしれません。
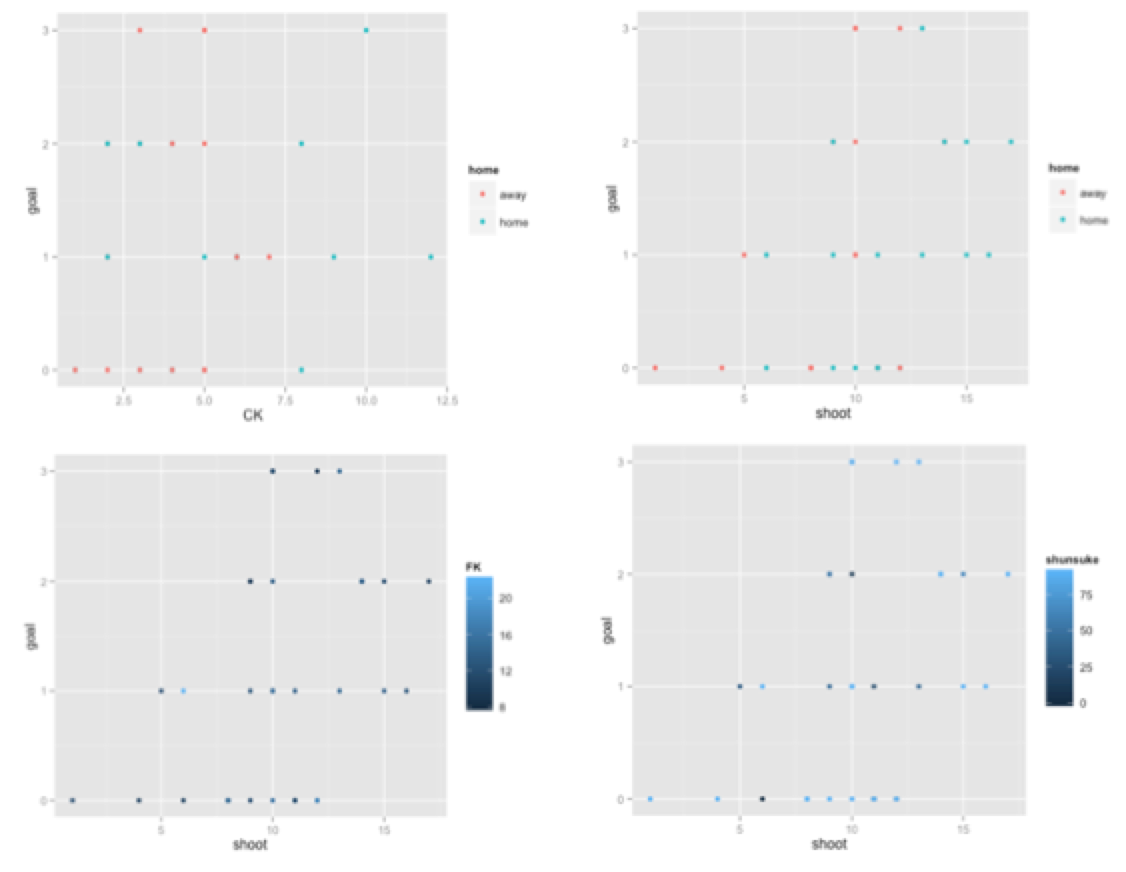
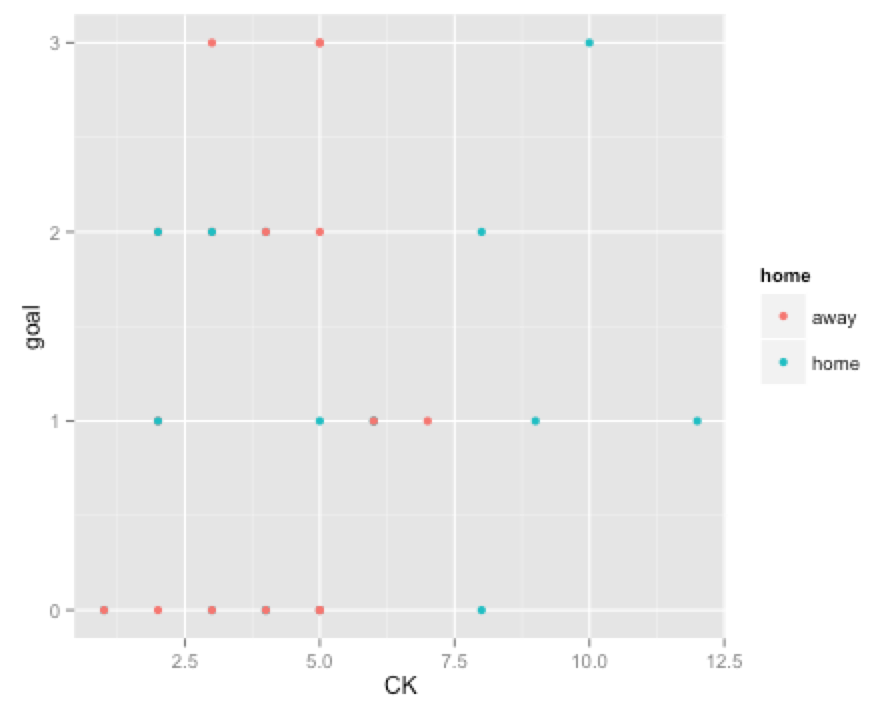
次に、shoot数や、CKやFKなどの変数も加味していきながら、散布図でも確認してみます。
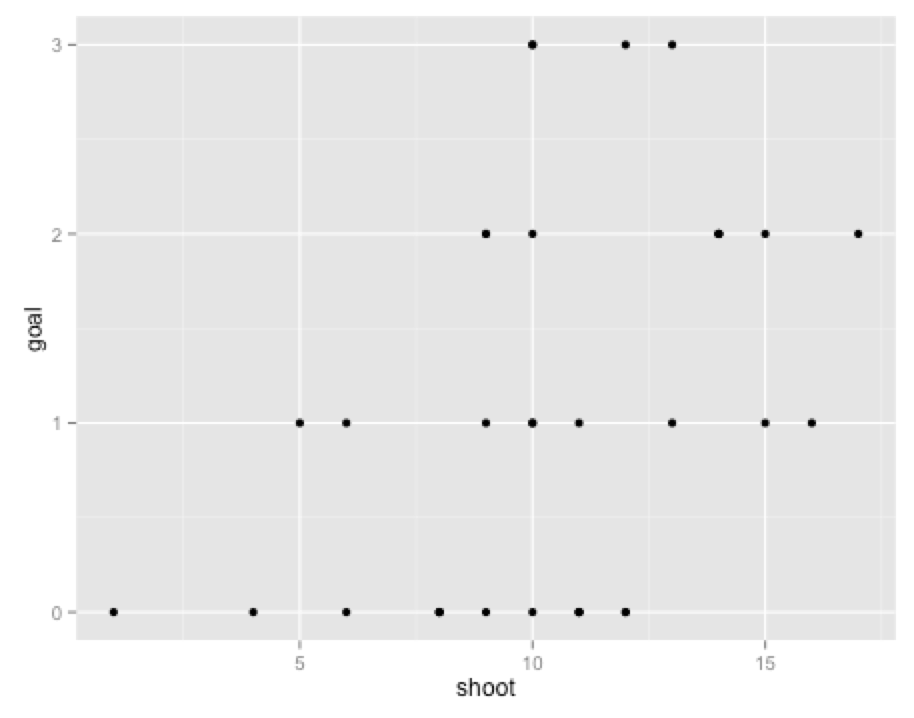
まずは、単純なshoot数ごとのゴール数の分布です。
|
1 2 3 |
g<-ggplot(marinosu,aes(x=shoot,y=goal)) g<-g+geom_point() plot(g) |
シュート数が増えるとゴール数が増える右肩上がりのグラフです。
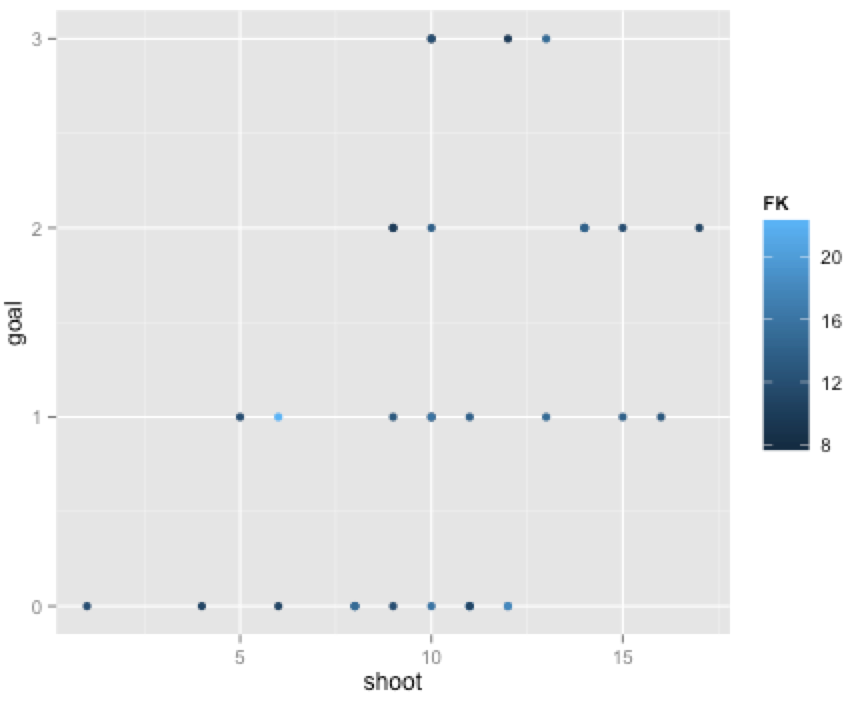
これをhome/awayでわけてみます。
|
1 2 3 |
g<-ggplot(marinosu,aes(x=shoot,y=goal)) g<-g+geom_point(aes(colour=home)) plot(g) |
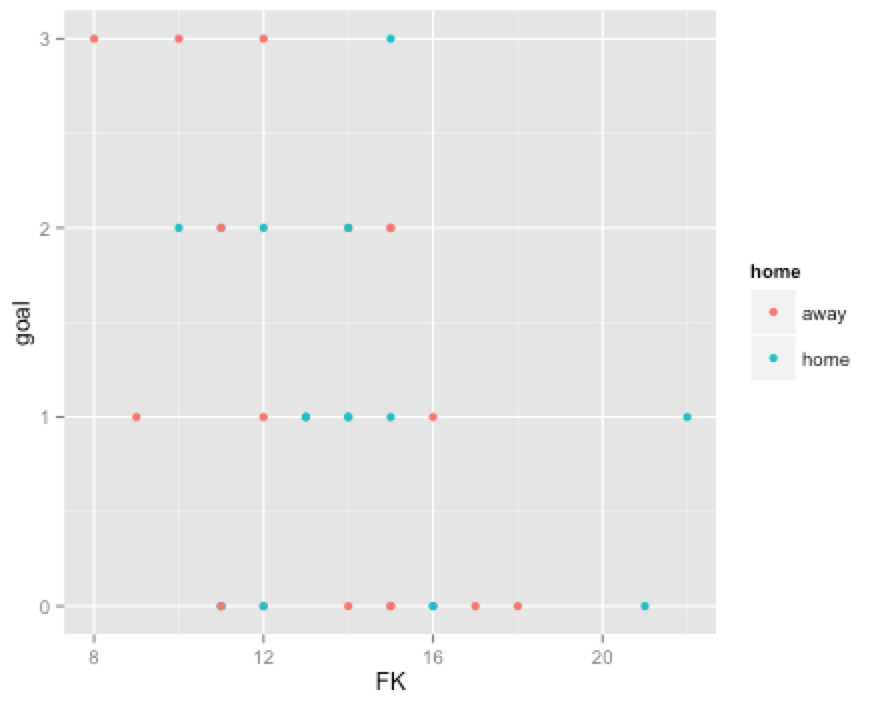
同様に、CKやFKなどでも確認してみます。
CKはやや相関ありそうですが、FKはゴールから遠い距離の場合もカウントされており、ゴールへの影響が少ないようです。
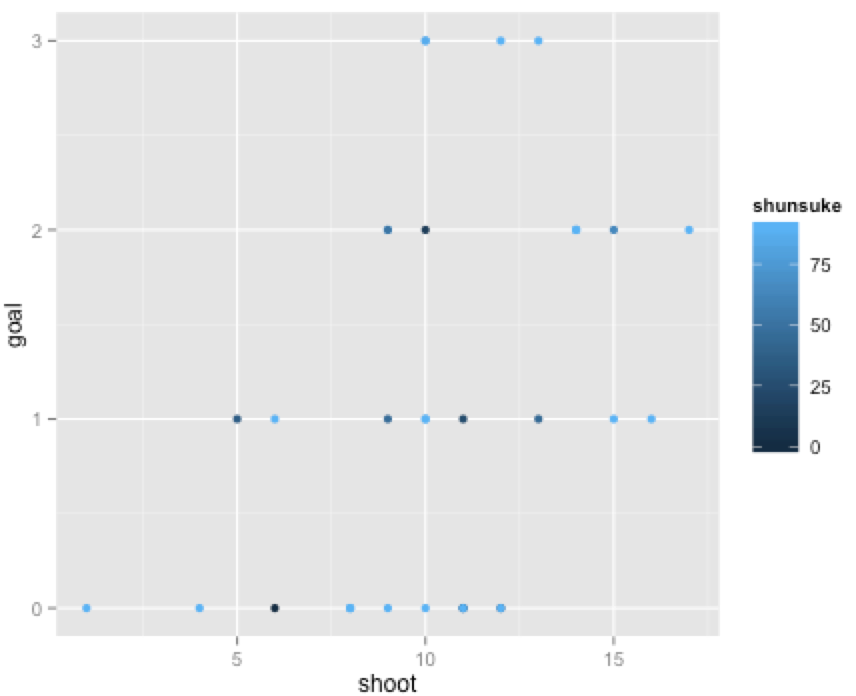
俊輔の出場時間も、一見、そこまでシュート数やゴール数に相関があるようには見えません。
さて、前置きが長くなりましたが、概要をplotで把握したところで、いよいよポワソン分布でモデリングしてみます。
「モデル1:ゴールは何にも影響を受けず一定の値をとるモデル」
「モデル2:ゴールはシュート数の影響を受けるモデル」
「モデル3:ゴールはシュート数に加えCKの影響を受けるモデル」
「モデル4:ゴールはシュート数に加えFKの影響を受けるモデル」
「モデル5:ゴールはシュート数に加えFK,home/awayの影響を受けるモデル」
「モデル6:ゴールはシュート数に加えFK,俊輔出場時間の影響を受けるモデル」
上記複数モデルの比較のための指標がAIC(Akaike Information Criterion)です。
ざっくり言うと、単純な「当てはまりの良さ」ではなく、
「出来るだけ少ないパラメータでまあまあ当てはまりが良いモデル」を選択出来ます。
これは、オーバーフィッティングなモデルを回避するために有効な指標となります。
RではAICを簡単に求めることができます。
Rのコードおよび、各モデルのAICは以下の通りです。
|
1 2 |
fit<-glm(formula=goal~shoot+home+FK,family=poisson,data=marinosu) fit |
| モデル | AIC |
| モデル1:ゴールは何にも影響を受けず一定の値をとるモデル | 95.17 |
| モデル2:ゴールはシュート数の影響を受けるモデル | 91.14 |
| モデル3:ゴールはシュート数に加えCKの影響を受けるモデル | 93.14 |
| モデル4:ゴールはシュート数に加えFKの影響を受けるモデル | 87.74 |
| モデル5:ゴールはシュート数に加えFK,home/awayの影響を受けるモデル | 87.87 |
| モデル6:ゴールはシュート数に加えFK,俊輔出場時間の影響を受けるモデル | 89.63 |
上記を見ていただいてわかる通り、「モデル4:ゴールはシュート数に加えFKの影響を受けるモデル」が、
最もAICが低い、つまり最低限のパラメータで当てはまりの良いモデル、となりました。
2014年度は、俊輔の直接FKからのゴールは0でしたが、FKの流れからのゴールはあったようで、
モデルの当てはまりにもあらわれております。
一方、CKからのゴールもあったと思いますが、単純にCKの数が多ければその分ゴールが増える、
というわけではないようです。
さらに詳細な、パス成功率やポゼッション率、などのオープンデータなどがあれば、
いろんな変数をかけあわせることができそうです。
いろんなモデルをポワソン分布で作ってAICで比較することがしたかったのですが、
大半の時間をマリノスのホームページからデータを集計する事に費やしてしまったため
むしろ、それ以降は、簡単なggplot2の使い方紹介、
およびモデリングのあてはめは、Rの1行で終わってしまいました。
※モデルの選択などの詳細は『データ解析のための統計モデリング入門』などが
参考になると思います。